多边形面积的计算方法
在几何学中,多边形是由三条或更多条直线段首尾顺次相连围成的封闭平面图形。计算多边形的面积是一项基础而重要的技能,它在建筑设计、土地测量、计算机图形学等多个领域都有广泛应用。本文将从多边形的基本分类出发,介绍几种常见多边形面积的计算方法,并探讨一些高级技巧及实际应用,旨在为读者提供一个全面而深入的理解。
一、多边形的基本分类与面积计算基础
多边形按边数可分为三角形、四边形、五边形等,其中三角形是最基础也是最重要的多边形,因为任何多边形都可以分割成若干个三角形来计算面积。根据边的性质,多边形又可分为规则多边形和不规则多边形。规则多边形各边等长,各内角相等,如正三角形、正方形;不规则多边形则不满足这些条件。
面积计算的基础在于理解图形的度量单位,对于平面图形而言,面积是以平方单位(如平方米、平方厘米)来衡量的。计算多边形面积的基本思路是将复杂图形分解为简单图形(尤其是三角形),然后分别计算再求和。
二、常见多边形面积的计算方法
1. 三角形面积的计算
三角形面积的计算有多种方法,最常用的是海伦公式和底乘高法。
海伦公式:适用于已知三边长度的三角形。设三角形三边分别为a、b、c,半周长p=(a+b+c)/2,则面积S=√(p(p-a)(p-b)(p-c))。
底乘高法:已知三角形底边长度b和高h,则面积S=(1/2)×b×h。
此外,还可以通过已知两边长和夹角、三边长和一角等条件,利用三角函数或余弦定理计算三角形面积。
2. 四边形面积的计算
四边形中,最常见的是矩形和平行四边形,其次是梯形和不规则四边形。
矩形面积:长l乘以宽w,即S=l×w。
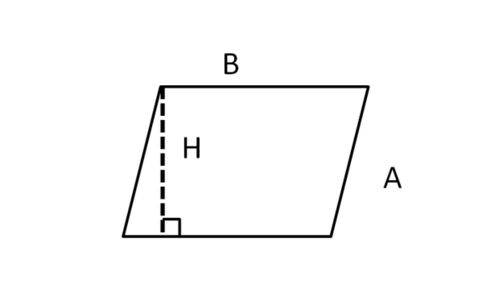
平行四边形面积:底b乘以高h,即S=b×h。这里的高是从平行四边形一边上任意一点到对边引垂线的长度。
梯形面积:上底a、下底b和高h已知时,面积S=(1/2)×(a+b)×h。
不规则四边形:通常可以通过划分成两个或多个三角形,分别计算面积后求和得到。
3. 规则多边形面积的计算
规则多边形因其对称性,面积计算相对简单。
正n边形面积:设边长为a,中心角为θ(θ=360°/n),面积S=(n/4)×a²×cot(θ/2)。对于正方形(n=4),面积简化为S=a²;对于正六边形,可视为由六个等边三角形组成,面积S=(3√3/2)×a²。
三、高级技巧:坐标几何法
在坐标几何中,多边形的面积可以通过顶点坐标来计算,这种方法特别适用于计算机编程和精确测量。
1. 三角形面积坐标公式
设三角形顶点坐标为A(x1,y1)、B(x2,y2)、C(x3,y3),则面积S=0.5×|x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|。
2. 多边形面积坐标公式
对于任意多边形,若按顶点顺序给出其顶点坐标(x1,y1)、(x2,y2)、...、(xn,yn)(最后一个顶点与第一个顶点重合形成闭环),则面积S=0.5×Σ[(xi+1-xi)×(yi+1+yi)],其中Σ表示求和,i从1遍历到n-1。
四、实际应用与注意事项
1. 土地测量
在土地测量中,多边形面积的计算对于确定地块大小、规划布局至关重要。实际应用中,可能需要结合GPS定位、遥感技术等现代技术手段,提高测量精度。
2. 计算机图形学
在计算机图形学中,多边形是构成复杂形状的基本单元。计算多边形面积不仅用于渲染效果的优化,还涉及碰撞检测、路径规划等多个方面。
3. 建筑设计
建筑设计中,计算多边形面积有助于合理规划空间布局,如房间面积、公共区域面积等,是设计规范和成本预算的重要依据。
注意事项
精度控制:无论是手工计算还是使用软件,都应关注精度问题,避免因四舍五入或测量误差导致的结果偏差。
单位统一:计算前确保所有尺寸数据使用相同的度量单位,避免单位转换错误。
方法选择:根据具体问题和条件选择合适的方法,如规则多边形可直接使用公式,不规则多边形则可能需要分割或采用坐标几何法。
五、结语
计算多边形面积不仅是一项基本的数学技能,更是连接理论与实践的桥梁。通过深入理解不同多边形的面积计算方法,我们能够更好地应用这些知识解决实际问题,无论是在学术研究、工程设计还是日常生活中。随着科技的进步,新的计算工具和方法不断涌现,但掌握基本原理和方法始终是理解和应用新知识的基础。希望本文能为读者提供一个清晰、全面的多边形面积计算指南,激发进一步探索的兴趣。
- 上一篇: 如何将中文翻译成英文
- 下一篇: 精致蒸排骨的制作方法
火爆游戏玩不停
新锐游戏抢先玩
游戏攻略帮助你
更多+-
02/08
-
02/08
-
02/08
-
02/08
-
02/08









