如何计算扇形的周长

扇形是圆的一个重要部分，通常由一个圆的两条半径和这两条半径之间的一段弧所围成。当我们想要计算扇形的周长时，需要了解几个关键的概念和公式。下面，我们将详细探讨扇形的周长如何求解，同时融入相关的关键词，以便提高文章的曝光率。

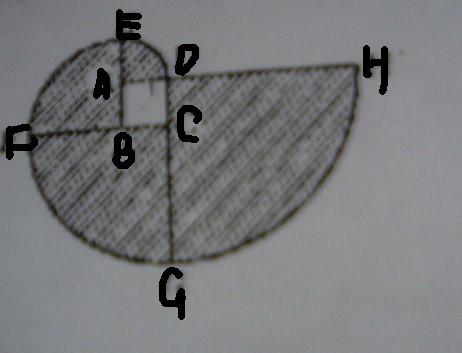
首先，我们需要明确扇形的定义及其组成部分。扇形是由圆心角、半径和弧组成的。圆心角是扇形顶点与圆心连线所夹的角，半径是从圆心到扇形顶点的线段，弧则是扇形两个顶点之间的圆上的一段曲线。扇形的周长，也称作扇形的边界长度，是由两条半径和一条弧组成的。

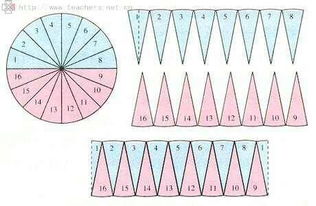
要求解扇形的周长，我们首先需要知道圆的周长和圆心角与整个圆周角（即360度）的比例关系。一个完整的圆的周长公式是C=2πr，其中C代表圆的周长，r代表圆的半径，π是一个数学常数，约等于3.14159。扇形是圆的一部分，因此扇形的弧长可以通过圆心角和整个圆周角的比例来计算。具体公式为：弧长=圆心角（以弧度为单位）/360°×2πr。

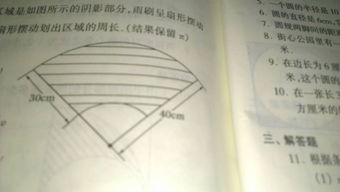
然而，在日常计算中，我们往往使用度数来表示圆心角，而不是弧度。为了将度数转换为弧度，我们可以使用公式：弧度=度数×π/180。因此，扇形弧长的计算公式也可以表示为：弧长=度数/180×π×2r。

现在，我们已经知道了如何计算扇形的弧长，接下来就可以求解扇形的周长了。扇形的周长由两条半径和一条弧组成，所以扇形的周长公式为：扇形周长=2r+弧长。将弧长的公式代入，我们得到：扇形周长=2r+（度数/180×π×2r）。

为了更具体地理解这个过程，我们可以举一个例子。假设我们有一个半径为5厘米的圆，我们要计算这个圆中圆心角为90度的扇形的周长。首先，我们计算扇形的弧长：弧长=90/180×π×2×5=5π厘米。然后，我们计算扇形的周长：扇形周长=2×5+5π=10+5π厘米。由于π约等于3.14159，所以我们可以将π的值代入公式，得到扇形周长的近似值：扇形周长≈10+5×3.14159=15.70795厘米。

在求解扇形周长的过程中，有几个重要的点需要注意。首先，确保你使用的是正确的半径和圆心角。半径是圆心到扇形顶点的距离，圆心角是扇形顶点与圆心连线所夹的角。其次，注意单位。如果圆心角是以度数给出的，你需要将其转换为弧度来计算弧长，但在这个特定的问题中，我们直接使用了一个将度数转换为弧长的公式，所以不需要进行额外的单位转换。最后，确保你的计算是准确的。由于π是一个无理数，所以你的计算结果可能会是一个无限不循环的小数。在实际应用中，我们通常会使用π的近似值（如3.14159）来进行计算。

此外，扇形周长的计算在几何学和工程学等领域有着广泛的应用。例如，在建筑设计中，扇形窗或扇形门的周长计算对于确定材料的使用量和成本至关重要。在工程学中，了解扇形的周长有助于设计旋转部件，如风扇叶片或涡轮机叶片，以确保它们能够高效地工作。

扇形的周长还与一些其他数学概念相关。例如，扇形的面积可以通过圆心角与整个圆周角的比例和圆的面积来计算。圆的面积公式是A=πr²，所以扇形的面积公式为：扇形面积=圆心角（以弧度为单位）/360°×πr²。虽然这与扇形的周长计算没有直接关系，但它展示了扇形与圆之间的一些基本联系。

另外，扇形还与一些更复杂的几何形状有关，如圆锥和圆柱。圆锥是由一个圆形底面和一个顶点不在底面上的点（称为圆锥的顶点）通过直线（称为圆锥的母线）连接而成的。圆锥的侧面展开后是一个扇形，所以扇形的周长计算对于理解圆锥的几何性质非常重要。同样地，圆柱的侧面也是一个矩形或平行四边形，但当它的一部分被切割时，可能会形成一个扇形形状。

总的来说，扇形的周长计算是一个涉及多个数学概念和公式的过程。通过了解扇形的组成部分、圆心角与弧长的关系以及如何使用这些关系来计算扇形的周长，我们可以更好地理解和应用这个概念。无论是在学术研究中还是在日常生活中，扇形的周长都是一个有用的工具，它可以帮助我们解决各种问题并理解世界的几何形状。因此，当你遇到与扇形周长相关的问题时，记得回顾这些概念和公式，并应用它们来找到解决方案。