揭秘！根号2的计算方法及结果

根号2等于多少怎么算

根号2，通常写作√2，是一个无理数，即它不能表示为两个整数的比。这意味着√2的小数部分是无限不循环的。要计算√2的值，可以使用多种方法，包括几何法、数列逼近法、计算器或数学软件等。

一、几何法

几何法是最直观的方法之一，它基于正方形的性质和勾股定理。

1. 构造正方形：

设想一个边长为1单位的正方形。这个正方形的面积是1平方单位。

2. 对角线长度：

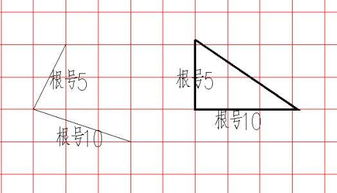
正方形的对角线将这个正方形分为两个相等的直角三角形。根据勾股定理，一个直角三角形的斜边（即对角线）的平方等于两直角边的平方和。在这个情况下，两直角边都是1单位，所以斜边的平方是1² + 1² = 2。

3. 定义√2：

由于对角线的平方是2，对角线的长度就是√2。因此，√2是这个正方形的对角线长度与边长之比。

二、数列逼近法

数列逼近法通过构造一系列越来越接近√2的数来逼近其真实值。这里介绍两种常用的数列逼近法：连分数法和牛顿迭代法。

1. 连分数法

连分数是一种表示无理数的特殊方式，它通过将数分解为一系列有理数的和来逼近无理数。对于√2，我们可以使用连分数展开式来逼近它。

√2的连分数展开式为：

√2 = 1 + (1/(2 + (1/(2 + (1/(2 + ...)))))

这是一个无限连分数，但我们可以取有限项来得到√2的近似值。例如，取前三项得到：

√2 ≈ 1 + 1/2 + 1/(2×3 + 2) = 1.4142135...

2. 牛顿迭代法

牛顿迭代法是一种快速收敛的数值方法，用于求解方程f(x) = 0的根。对于√2，我们可以将其表示为方程x² - 2 = 0的根。

牛顿迭代法的迭代公式为：

x_(n+1) = x_n - f(x_n)/f'(x_n)

在这里，f(x) = x² - 2，f'(x) = 2x。

选择初始值x_0（例如x_0 = 1），然后应用迭代公式进行多次迭代，直到得到足够精确的√2的近似值。

三、计算器或数学软件

在现代社会中，计算器或数学软件是求解√2等无理数的便捷工具。

1. 计算器：

大多数计算器都有开方功能，可以直接输入“2”然后按下开方键（通常标记为√或^0.5）来得到√2的值。

2. 数学软件：

数学软件如Mathematica、MATLAB、Python的NumPy库等，提供了更强大的数值计算和符号计算能力。在这些软件中，可以直接输入sqrt(2)来得到√2的精确值或任意精度的近似值。

四、√2的精确值

虽然√2是一个无理数，无法表示为两个整数的比，但我们可以使用计算器或数学软件来得到其精确值（在给定精度下）。

√2 ≈ 1.41421356237309504880168872420969807856967187537694807317667973799...

这个值是在计算过程中截取的一部分，实际上√2的小数部分是无限不循环的。

五、实际应用

√2在日常生活和科学研究中有着广泛的应用。

1. 几何与建筑：

在建筑和设计中，√2的比例关系经常出现。例如，在黄金分割和斐波那契数列中，√2起着重要作用。这些比例关系在美学和功能性上都具有重要意义。

2. 物理学：

在物理学中，√2经常出现在各种公式和定律中。例如，在电磁学和量子力学中，√2与波函数的归一化和概率计算有关。

3. 计算机科学：

在计算机科学中，√2用于算法分析和数据结构设计。例如，在哈希函数和搜索算法中，√2的比例关系可以优化性能。

六、总结

根号2（√2）是一个无理数，表示一个边长为1单位的正方形的对角线长度。要计算√2的值，可以使用几何法、数列逼近法、计算器或数学软件等方法。虽然√2无法表示为两个整数的比，但我们可以使用这些方法来得到其精确值（在给定精度下）或近似值。在实际应用中，√2在几何、建筑、物理学和计算机科学等领域都有着广泛的应用。

√2 ≈ 1.41421356237309504880168872420969807856967187537694807317667973799...