互质数的定义与含义

互质数，这一概念在数学领域中占据着举足轻重的地位，尽管它听起来可能有些抽象，但实则在我们的日常生活中有着广泛的应用。简而言之，互质数是指两个或多个整数共有的唯一正因数只有1的数对或数组。换句话说，如果两个数的最大公约数为1，则这两个数互为互质数。这一特性使得互质数在数论、密码学、计算机科学等多个领域都发挥着重要作用。

首先，让我们深入了解一下互质数的定义。两个或多个整数，如果它们之间除了1以外没有其他公因数，则称这些数为互质数。例如，8和15就是一对互质数，因为它们的公约数只有1。同样地，一组数如3、4和5也是互质的，因为它们之间也没有其他公约数。互质数的概念可以扩展到任意数量的整数，只要这些数的最大公约数为1，它们就可以被视为互质数。

在探讨互质数的性质时，我们会发现几个有趣的特点。首先，任何两个质数都是互质的。这是因为质数本身只能被1和自身整除，所以两个质数之间不可能有除了1以外的公因数。例如，2和3、11和13等都是互质的质数对。其次，如果一个数是质数，而另一个数不是该质数的倍数，则这两个数也是互质的。这是因为如果一个数不是另一个质数的倍数，那么它们之间除了1以外没有其他公因数。例如，3和10就是互质的，因为10不是3的倍数。

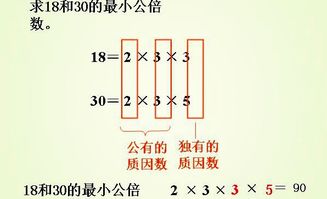
互质数在数学中的应用广泛而深入。在数论中，互质数是研究整数性质的重要工具。例如，在求两个数的最小公倍数时，如果这两个数是互质的，那么它们的最小公倍数就是它们的乘积。这是因为互质数的最小公倍数等于它们的乘积除以它们的最大公约数，而互质数的最大公约数为1，所以最小公倍数就等于它们的乘积。这一性质在解决实际问题时非常有用，例如在计算分数的最小公倍数时，如果分数的分母是互质的，那么它们的最小公倍数就等于这些分母的乘积。

在密码学中，互质数也扮演着重要的角色。例如，在RSA加密算法中，就需要用到大素数和大素数的乘积。这些大素数和大素数的乘积之间的互质性保证了加密算法的安全性。因为攻击者要破解这个加密算法，就需要找到这些大素数的因数，而这是一个非常困难的问题。因此，互质数在密码学中提供了一种有效的加密手段，保护了我们的信息安全。

此外，互质数在计算机科学中也有广泛的应用。例如，在解决某些优化问题时，我们需要找到一组互质的数来构造最优解。这些互质的数可以帮助我们避免重复计算，提高算法的效率。同时，在随机数生成算法中，互质数也被用来确保生成的随机数是均匀分布的，从而提高算法的随机性和安全性。

在实际生活中，互质数的应用同样丰富多彩。例如，在编排班级座位时，如果老师希望每个学生都有一个不同的座位号，并且这些座位号之间尽可能地没有重复的数字，那么他们可以选择一组互质的数字作为座位号。这样，即使有一些学生选择相同的数字作为自己的幸运数字，但由于这些数字是互质的，所以它们之间不会重复，从而保证了座位号的唯一性。

另外，在编排音乐节奏时，互质数也发挥着重要的作用。如果作曲家希望创造出一种独特的节奏模式，他们可以选择一组互质的数字作为节奏的基本单位。这样，即使这些节奏在听觉上可能没有明显的差异，但由于它们之间不存在共同的节奏周期，所以它们能够产生出一种独特的音乐效果。

当然，互质数的应用还远远不止这些。在统计学、物理学、化学等其他学科中，我们都可以找到互质数的身影。它们作为数学中的一种基本工具，为这些学科的研究提供了有力的支持。

在探索互质数的历史时，我们会发现这一概念有着悠久的历史和深厚的文化底蕴。早在古代，数学家们就开始研究互质数的性质和应用。他们通过不断的实践和总结，逐步形成了今天我们所熟悉的互质数理论。这些研究成果不仅丰富了数学宝库，也为其他学科的发展提供了有力的数学工具。

总之，互质数是一个既简单又复杂的数学概念。它简单在于它的定义和性质都非常直观和易于理解；它复杂在于它在数学、密码学、计算机科学等领域中的广泛应用和深入研究。通过对互质数的学习和研究，我们可以更好地理解数学中的许多基本概念和原理，同时也可以为我们解决实际问题提供有力的数学支持。因此，无论是在学术研究还是在实际应用中，互质数都值得我们深入研究和探索。