多边形的内角和如何计算？

在我们日常生活中，无论是数学课本上，还是建筑、艺术设计中，多边形都无处不在。从简单的三角形到复杂的十边形、二十边形，它们都有着各自的美丽与奥秘。而今天，我们要深入探讨的，就是多边形的一个重要属性——内角和。

多边形的内角和是什么？

首先，让我们明确一下什么是多边形的内角和。多边形是由至少三条直线（称为边）首尾相连，且所有内角都小于180度所组成的平面图形。多边形的每一个内角，就是两条相邻边所夹的角。而多边形的内角和，就是所有这些内角的总和。

为什么计算多边形的内角和很重要？

计算多边形的内角和，不仅能帮助我们解决数学问题，还在很多实际领域有着广泛的应用。比如，在建筑设计中，设计师需要确保建筑物的每个角度都准确无误，以保证结构的稳定性和美观性。在计算机图形学中，理解多边形的内角和有助于开发更加精准的图像渲染和三维建模技术。此外，在数学教学中，掌握这一知识也是培养学生逻辑思维和几何直觉的重要途径。

如何计算多边形的内角和？

现在，让我们来揭开计算多边形内角和的神秘面纱。实际上，无论多边形有多少条边，我们都可以通过一个简单而巧妙的公式来求解。

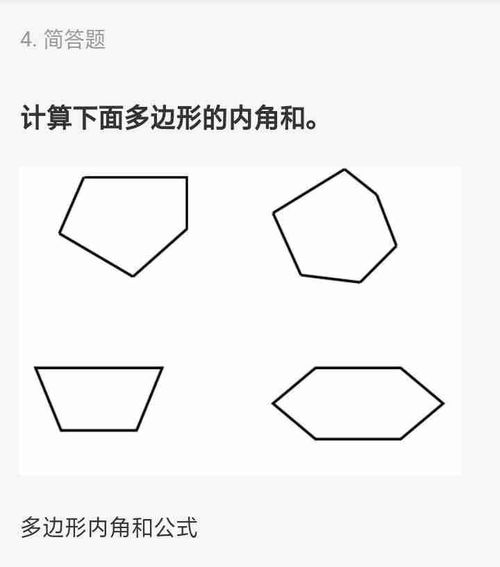
公式推导

想象一下，一个三角形。它的内角和是多少呢？没错，是180度。这是我们计算多边形内角和的基础。

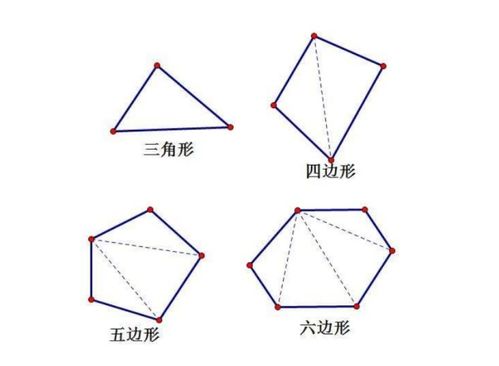
那么，当我们增加一个边，形成一个四边形时，我们可以把它看作是一个三角形加上一个三角形（通过从一个顶点引出对角线将其分割）。这样，四边形的内角和就是两个三角形的内角和之和，即180度+180度=360度。

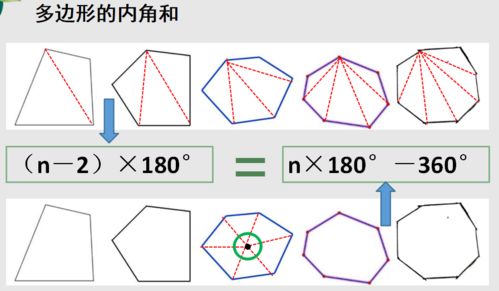
以此类推，每当我们增加一个边，就多出一个三角形。因此，多边形的内角和可以看作是由(n-2)个三角形组成的，其中n是多边形的边数。

所以，多边形内角和的公式就是：

内角和 = (n - 2) × 180度

这个公式非常简洁且实用，只要我们知道多边形的边数，就能迅速计算出它的内角和。

实际应用

接下来，让我们通过几个例子来进一步理解这个公式。

1. 五边形

五边形有5条边。根据公式，它的内角和为：

(5 - 2) × 180度 = 3 × 180度 = 540度

2. 八边形

八边形有8条边。同样地，使用公式计算得到：

(8 - 2) × 180度 = 6 × 180度 = 1080度

3. 不规则多边形

值得注意的是，这个公式不仅适用于规则多边形（如正五边形、正八边形等），也适用于不规则多边形（即各边和各角都不相等的多边形）。只要我们知道不规则多边形的边数，就可以用这个公式来求解它的内角和。

如何验证计算结果？

为了确保我们的计算准确无误，我们还可以采用另一种方法来验证多边形的内角和。这种方法适用于我们能够准确测量多边形每个内角的情况。

具体步骤如下：

1. 使用量角器或相关工具，分别测量多边形的每个内角。

2. 将所有测量得到的内角相加，得到总和。

3. 比较这个总和与我们使用公式计算得到的结果。如果两者相等（或相差在合理范围内，考虑到测量误差），则说明我们的计算是正确的。

常见问题解答

Q1：为什么三角形的内角和总是180度？

A1：这是一个几何学的基本定理，可以通过多种方法证明。其中一种常见的方法是使用平行线定理和同位角性质。简而言之，就是将三角形的一个角转化为另外两个角的补角，然后通过平行线的性质证明这三个角之和为180度。

Q2：多边形的外角和是多少？

A2：与内角和不同，多边形的外角和是一个常数，与多边形的边数无关。对于任何多边形，它的外角和总是360度。这是因为我们可以从多边形的任意一个顶点出发，逆时针或顺时针依次测量每个外角，并将它们相加。由于多边形是封闭的，所以这些外角最终会构成一个完整的圆周角，即360度。

Q3：如何快速找到多边形的一个内角？

A3：如果我们知道多边形的内角和以及除了一个内角之外的所有其他内角的度数，那么我们可以使用内角和公式反推出这个未知的内角。具体做法是：先用公式计算出多边形的内角和，然后从总和中减去已知的其他内角的度数之和，即可得到未知的内角的度数。

结语

通过以上的讲解和例子，相信你已经对如何计算多边形的内角和有了深入的了解。这个看似简单的公式背后，蕴含着丰富的几何原理和广泛的应用价值。无论是在数学学习中，还是在日常生活的各个领域，掌握这一知识都将为我们带来更多的便利和乐趣。

最后，我想说的是，数学并不是一门枯燥乏味的学科。只要我们用心去发现、去探索，就能在其中找到无穷的乐趣和奥秘。希望这篇文章能够激发你对数学的兴趣和热情，让你在数学的道路上越走越远！