初三数学:如何计算正弦值、余弦值和正切值?
初三数学中,三角函数是一个重要的知识点,其中正弦值、余弦值和正切值是三角函数的基础。在直角三角形中,通过定义这些比值,我们可以解决许多与角度和边长相关的问题。下面将详细介绍正弦值、余弦值和正切值的定义、性质及其在解题中的应用。
mdash mdash

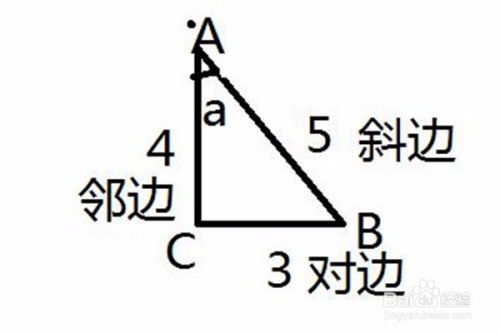
在直角三角形中,任意一锐角A的对边记为a,邻边记为b,斜边记为c。根据三角函数的定义,我们有:
正弦值(sine):sinA = a/c
正弦值表示的是对边与斜边的比值。在0°到90°的范围内,正弦值随着角度的增大而增大。当角度为0°时,sin0°=0;当角度为90°时,sin90°=1。正弦函数在第一象限和第二象限为正,在第三象限和第四象限为负。
余弦值(cosine):cosA = b/c
余弦值表示的是邻边与斜边的比值。在0°到90°的范围内,余弦值随着角度的增大而减小。当角度为0°时,cos0°=1;当角度为90°时,cos90°=0。余弦函数在第一象限和第四象限为正,在第二象限和第三象限为负。
正切值(tangent):tanA = a/b
正切值表示的是对边与邻边的比值。在0°到90°的范围内,正切值随着角度的增大而增大。当角度为0°时,tan0°=0;当角度接近90°时,正切值趋向于无穷大(但不存在)。正切函数在第一象限和第三象限为正,在第二象限和第四象限为负。
了解了正弦值、余弦值和正切值的定义后,我们可以进一步探讨它们在解题中的应用。
一、利用三角函数求角度
在实际问题中,我们经常会遇到已知三角形两边长,需要求解角度的情况。此时,可以利用三角函数表或计算器,通过比值反求角度。例如,已知直角三角形中,对边长为3,斜边长为5,则可以通过sinA = 3/5求出角A的度数。
二、利用三角函数求边长
在已知角度和一边长的情况下,我们可以利用三角函数求出另一边长。例如,在直角三角形中,已知角A为30°,斜边长为10,则可以通过cos30° = b/10求出邻边长b的值。
三、利用三角函数解决实际问题
三角函数在解决实际问题中有着广泛的应用。例如,在建筑设计中,我们需要计算建筑物的高度或倾斜角度;在航海中,我们需要计算船只的航向或距离;在物理学中,我们需要计算物体的运动轨迹或速度等。这些问题都可以通过构建直角三角形,利用三角函数进行求解。
此外,三角函数还与圆的性质密切相关。在单位圆上,任意一点P的坐标可以表示为(cosθ, sinθ),其中θ为点P与x轴正方向的夹角。这一性质使得三角函数在解析几何、复数等领域中也有着广泛的应用。
在初三数学的学习中,我们还需要掌握三角函数的一些基本性质。例如,同角三角函数的基本关系式:sin²A + cos²A = 1;正切与正弦、余弦的关系式:tanA = sinA/cosA。这些关系式在解题中经常用到,可以帮助我们简化计算或证明题目。
同时,我们还需要了解三角函数的图像和性质。正弦函数、余弦函数和正切函数的图像都是周期函数,具有周期性、奇偶性等性质。这些性质在解题中也有着重要的应用。例如,在求解三角函数的最值、零点等问题时,我们可以利用这些性质进行求解。
在备考初三数学时,我们还需要注意以下几点:
1. 熟练掌握三角函数的定义、性质和基本关系式,能够灵活运用它们进行解题。
2. 多做练习题,尤其是与三角函数相关的综合应用题,提高自己的解题能力和思维灵活性。
3. 认真阅读教材和相关资料,理解三角函数的本质和意义,加深对三角函数的理解和掌握。
4. 学会利用计算器或三角函数表进行求解,提高解题效率和准确性。
5. 注意总结归纳解题方法和技巧,形成自己的解题思路和方法体系。
通过初三数学中对正弦值、余弦值和正切值的学习,我们可以更好地掌握三角函数这一重要知识点,为解决实际问题提供有力的数学工具。同时,三角函数的学习也有助于培养我们的逻辑思维能力和数学素养,为未来的学习和工作打下坚实的基础。
mdash mdash
希望以上内容能够帮助你更好地理解和掌握初三数学中正弦值、余弦值和正切值的相关知识。在学习的过程中,要注重理论与实践相结合,多做练习题,加深对知识点的理解和掌握。同时,也要保持积极的学习态度和良好的学习习惯,不断提高自己的数学素养和解题能力。
- 上一篇: 如何查看京东物流信息
- 下一篇: What Does 'Receive' Mean?
火爆游戏玩不停
新锐游戏抢先玩
游戏攻略帮助你
更多+-
01/31
-
01/31
-
01/31
-
01/31
-
01/31









