探索勾股定理的多样证明途径
勾股定理,一个基础且实用的数学定理,指的是直角三角形的两条直角边的平方和等于斜边的平方。这个定理的证明方法多种多样,每一种方法都蕴含着深刻的数学思想和智慧。本文将详细介绍勾股定理的多种证明方法,帮助读者深入理解这一定理的本质。
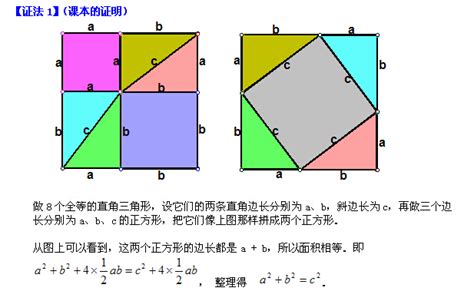
几何证明法
1. 赵爽弦图法
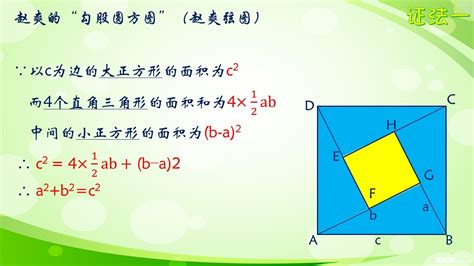
赵爽弦图是中国汉代数学家赵爽在注解《周髀算经》时提出的一种证明方法。这种方法通过切割和重拼图形来证明勾股定理。具体步骤如下:
构造四个全等的直角三角形,以它们为边构成一个大的正方形。
中间留下一个小的正方形空洞。
通过计算和比较四个直角三角形的面积与大正方形及小正方形的面积关系,可以证明勾股定理。
赵爽弦图法通过直观的拼图展示了勾股定理的几何意义,无需复杂的代数运算,是一种简单而优美的证明方法。
2. 构造正方形法
构造一个边长为直角边a和b之和的正方形,然后在其中构造两个以a和b为边长的小正方形。通过计算这三个正方形的面积关系,可以证明勾股定理。
大正方形的面积为(a+b)²。
两个小正方形的面积分别为a²和b²。
剩余部分由四个全等的直角三角形组成,它们的面积之和为c²(斜边c的平方)。
通过计算得出(a+b)²-a²-b²=c²,即勾股定理。
代数证明法
1. 平方公式法
利用代数的平方公式,直接将直角三角形的三边平方代入勾股定理的式子中进行证明。
设直角三角形的两条直角边为a和b,斜边为c。
根据勾股定理,有a²+b²=c²。
通过代数运算和因式分解等方法,可以证明该式成立。
2. 数学归纳法
数学归纳法是一种证明序列命题的方法,也可以用于证明勾股定理。
首先证明当n=1时,勾股定理成立。
然后假设当n=k时,勾股定理成立。
证明当n=k+1时,勾股定理依然成立。
通过数学归纳法,可以证明对于所有正整数n,勾股定理都成立。
物理证明法
力学原理法
利用力学原理,假设一个质点在平面上运动,其两个方向上的速度分量分别为a和b,斜向速度c可以表示为(a²+b²)的平方根。
根据速度的合成与分解原理,有c²=a²+b²。
这与勾股定理的公式形式完全一致,从而证明了勾股定理。
微积分证明法
连续性证明
使用微积分的概念,将直角三角形的斜边分成许多小段,当这些小段越来越小,相应的直角边也会越来越小,直到变得可以忽略不计。
通过微积分中的极限概念,可以证明直角三角形的两条直角边的平方和等于斜边的平方。
这种方法虽然较为复杂,但提供了一种从连续性和极限角度理解勾股定理的新视角。
其他证明方法
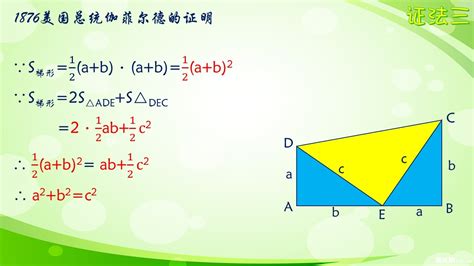
1. 相似三角形法
通过构造相似的三角形,利用相似三角形的性质来推导勾股定理。
构造一个直角三角形和一个与之相似的三角形。
通过计算两个三角形的边长比例和面积关系,可以证明勾股定理。
2. 向量证明法
利用向量的几何意义和点积公式来证明勾股定理。
首先计算向量的长度和夹角。
然后利用向量的点积公式计算勾股定理中的各个变量。
最后推导出勾股定理。
3. 割圆术法
利用割圆术将直角三角形的对角线作为半径画圆,通过圆上弧角定理来证明勾股定理。
这种方法涉及较为复杂的几何构造和圆上弧角的计算。
但通过巧妙的构造和计算,可以证明勾股定理的正确性。
4. 解析几何法
利用平面直角坐标系来证明勾股定理。
将直角三角形的三个点用坐标表示出来。
通过计算坐标之间的距离和关系,可以证明勾股定理。
5. 三角函数法
利用三角函数的性质来证明勾股定理。
将三角形分离出直角三角形和非直角三角形。
通过三角函数计算出各个变量的值。
最后推导出勾股定理。
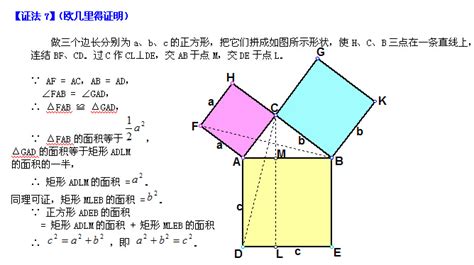
6. 古希腊证明法
古希腊人对勾股定理有独特的证明方法。
他们通过构造几何图形,利用几何图形的形状和大小关系来推导勾股定理。
这种方法体现了古希腊数学中的演绎法和几何直觉。
总结
勾股定理是一个既基础又重要的数学定理,具有广泛的应用。通过上述多种证明方法,我们可以从不同的角度和层面深入理解这一定理的本质。无论是几何证明、代数证明、物理证明还是微积分证明,每一种方法都展示了数学思想的多样性和深刻性。掌握这些证明方法不仅有助于提升数学素养和逻辑思维能力,还能在日常生活和工作中发挥重要作用。希望本文能够帮助读者更好地理解和应用勾股定理。
- 上一篇: 微信电话铃声个性化设置指南
- 下一篇: 揭秘!北京邮政编码大全,快速查询就在这里!
新锐游戏抢先玩
游戏攻略帮助你
更多+-
03/03
-
03/03
-
03/03
-
03/03
-
03/03









