置信区间如何计算？公式揭秘！

置信区间，作为统计学中的一个核心概念，为我们提供了一种估计总体参数范围的方法。当我们无法对全部样本进行统计时，通常会选择抽样调查，而抽样得到的结果只是对总体真实值的估计。为了更好地理解这个估计的准确性和可靠性，置信区间应运而生。它不仅能够给出估计的参数值，还能提供一个范围，告诉我们这个估计值有多大的可能性落在该范围内。下面，我们就来详细介绍一下置信区间的计算公式及其相关方面。

置信区间的基本概念

首先，需要明确的是，置信区间是为参数估计服务的。例如，我们想要估计某个国家的平均工资水平，但无法统计所有人的工资，这时我们会进行抽样调查。通过抽样得到的结果，我们可以计算出样本的均值，但这个均值可能并不能很好地代表整个国家的工资水平。因此，我们需要一个范围，即置信区间，来表示这个估计值的可靠性。

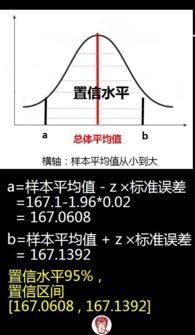
置信区间实际上包含两个值：置信上界和置信下界。当我们说某个参数的95%置信区间是[a, b]时，意味着如果我们进行100次抽样并计算置信区间，有95次这些区间会包含总体的真实参数值。

置信区间的计算公式

置信区间的计算公式通常为：置信区间 = 点估计值 ± (可靠性系数 × 标准误差)。这里的点估计值是基于样本数据得出的总体参数的最佳估计，可靠性系数（也称为置信系数）反映了置信区间的可靠程度，标准误差则是衡量估计精度的一个指标。

1. 基于正态分布的置信区间

当总体方差已知且样本量较大（通常大于30）时，可以使用基于正态分布的置信区间公式。在这种情况下，可靠性系数可以通过查找正态分布表得到，通常使用的是Z分数。例如，95%的置信水平对应的Z分数约为1.96。

公式为：CI = 样本均值 ± Z分数 × (总体标准差 / √样本量)。

2. 基于t分布的置信区间

当总体方差未知且样本量较小（小于30）时，应使用t分布来计算置信区间。t分布是当样本量较小时，样本均值与总体均值之间差异的分布，它比正态分布更加“扁平”。

公式为：CI = 样本均值 ± tα/2,n-1 × (样本标准差 / √样本量)。这里的tα/2,n-1是通过查找t分布表得到的。

3. 单边置信区间

有时候，我们只对参数的一侧感兴趣，例如，我们可能只想知道一个参数的最小可能值或最大可能值。这时，我们可以使用单边置信区间。

单边下限公式：CI下限 = 点估计值 - 可靠性系数 × 标准误差。

单边上限公式：CI上限 = 点估计值 + 可靠性系数 × 标准误差。

4. 贝努瓦-切比雪夫不等式置信区间

当需要估计参数的置信区间，并且对置信水平要求较高时，可以使用贝努瓦-切比雪夫不等式置信区间。这个不等式提供了一个比较保守但较为简单的置信区间估计方法。

公式为：CI = 参数估计值 ± k × 参数估计的标准差。这里的k是一个与置信水平相关的常数。

置信区间的选择与解释

选择合适的置信区间公式取决于多种因素，包括总体方差是否已知、样本量大小以及所需的置信水平等。在实际应用中，95%和99%的置信水平最为常见。

95%置信水平：意味着如果我们进行100次抽样并计算置信区间，有95次这些区间会包含总体的真实参数值。

99%置信水平：意味着如果我们进行100次抽样并计算置信区间，有99次这些区间会包含总体的真实参数值。但需要注意的是，99%的置信区间通常会比95%的置信区间更宽。

置信区间的宽度受多种因素影响，包括样本量、总体方差以及置信水平。一般来说，样本量越大，置信区间越窄；总体方差越大，置信区间越宽；置信水平越高，置信区间也越宽。

置信区间的应用

置信区间在统计学和实际应用中具有广泛的应用。例如：

市场调研：通过抽样调查估计消费者对某产品的满意度，并给出置信区间来评估这个估计的可靠性。

医学研究：在药物试验中，通过计算置信区间来评估药物的疗效和安全性。

工程质量控制：在生产过程中，通过抽样检测产品的质量指标，并计算置信区间来评估整体产品的质量水平。

如何计算置信区间

要计算置信区间，通常需要以下几个步骤：

1. 确定样本均值和样本标准差：这是基于样本数据计算得到的。

2. 确定置信水平：选择所需的置信水平，如95%或99%。

3. 查找可靠性系数：根据置信水平和样本量查找对应的可靠性系数（Z分数或t分数）。

4. 计算标准误差：使用样本标准差和样本量计算标准误差。

5. 计算置信区间：将上述值代入置信区间的公式中计算结果。

置信区间与置信度的关系

置信区间与置信度之间密切相关。置信度反映了我们对置信区间包含总体真实参数值的信心程度。例如，95%的置信度意味着我们有95%的信心认为总体真实参数值落在我们计算的置信区间内。

需要注意的是，置信区间是一个估计范围，而不是确定性的结论。它只能告诉我们参数值有多大可能性落在某个范围内，而不能给出确切的参数值。

结语

置信区间是统计学中一个非常重要的概念，它为我们提供了一种估计总体参数范围的方法。通过选择合适的置信区间公式并正确计算置信区间，我们可以更好地了解抽样结果的准确性和可靠性。无论是在市场调研、医学研究还是工程质量控制等领域，置信区间都具有广泛的应用价值。希望本文能够帮助读者更好地理解和应用置信区间的计算公式及其相关知识。