正方形有哪些常用的公式？

正方形的奇妙世界：揭秘那些简单却强大的公式

在几何学的浩瀚宇宙中，正方形以其独特的对称美和简洁性，始终占据着举足轻重的地位。它不仅是孩子们初识几何图形的起点，也是数学家们探索形状奥秘的重要对象。那么，正方形的公式是什么呢？这不仅仅是一个简单的数学问题，更是一次深入探索正方形神秘魅力的旅程。

首先，让我们从最基本的定义出发。正方形是一种四边形，它的四条边长度相等，四个角都是直角。这个简单的定义背后，隐藏着无数有趣的数学性质和公式。

面积公式：正方形的核心魅力

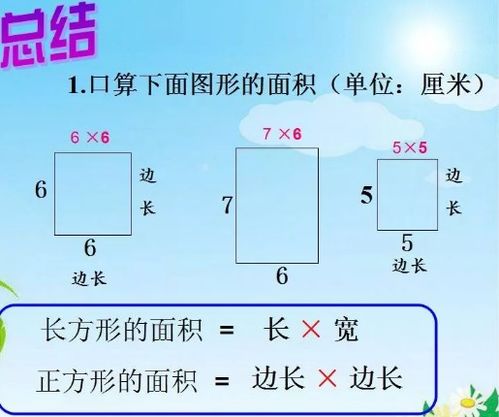
提到正方形的公式，最绕不开的当属面积公式。正方形的面积计算公式简洁而直观：边长乘以边长，即S=a²。这个公式不仅易于记忆，而且在实际生活中有着广泛的应用。无论是装修房间计算瓷砖数量，还是园艺设计估算花坛面积，正方形的面积公式都能轻松应对。

想象一下，你站在一个正方形的花园里，每走一步都恰好是花园边长那么长。那么，你只需要知道这一步的长度，就能迅速算出整个花园的面积。是不是觉得既神奇又实用呢？

周长公式：正方形的边界艺术

除了面积，正方形的周长也是一个重要的几何量。周长是指图形所有边的长度之和。对于正方形来说，由于它的四条边都相等，所以周长公式就显得格外简单：周长P=4a。这个公式告诉我们，只要知道正方形的边长，就能立刻算出它的周长。

周长公式在生活中的应用同样广泛。比如，在制作一个正方形的相框时，你需要知道相框的周长来购买合适长度的木条。或者，在布置一个正方形的展览区域时，周长公式能帮助你准确计算所需的围栏长度。

对角线公式：正方形的内在连接

正方形的对角线也是一个不可忽视的几何量。对角线是指连接正方形相对两个顶点的线段。正方形的对角线不仅长度相等，而且互相垂直平分。对角线的长度公式是：d=√2a（其中d表示对角线长度，a表示边长）。

这个公式虽然比面积和周长公式稍微复杂一些，但它揭示了正方形内部的一种深刻联系。通过对角线，我们可以发现正方形与直角三角形之间的微妙关系。事实上，正方形的对角线将正方形分为了两个完全相等的直角三角形，而这两个直角三角形的斜边就是正方形的对角线。

对角线公式在解决一些几何问题时非常有用。比如，在计算正方形内接圆的半径或外接圆的半径时，对角线公式就能提供关键的信息。

正方形的性质与公式的关系

正方形的许多性质都可以通过它的公式来体现。比如，正方形的对称性就体现在它的面积、周长和对角线公式中。这些公式都是基于正方形边长相等的这一基本性质推导出来的。

此外，正方形的内角和性质也与它的公式密切相关。正方形的内角和是360度，这意味着正方形的四个角都是直角。这一性质在推导正方形的面积公式时起到了关键作用。因为只有当四个角都是直角时，我们才能将正方形看作是由四个完全相等的直角三角形组成的。

正方形公式的应用实例

正方形的公式在现实生活中有着广泛的应用。以下是一些具体的例子：

1. 建筑设计：在建筑设计中，正方形公式经常被用来计算房间的面积和周长。比如，在规划一个正方形的会议室时，设计师需要知道会议室的面积来确定座位数量；同时，他们还需要知道会议室的周长来安排门窗的位置和大小。

2. 园艺设计：园艺设计师在规划花坛时，也经常会用到正方形的公式。通过计算花坛的面积和周长，设计师可以确定花坛的大小和形状，以及需要种植的花卉数量和种类。

3. 电子电路设计：在电子电路设计中，正方形公式也扮演着重要角色。比如，在设计一个正方形的集成电路板时，工程师需要知道电路板的面积来确定可以放置的元件数量；同时，他们还需要知道电路板的周长来安排连接线的走向和长度。

4. 游戏设计：在游戏设计中，正方形公式同样有着广泛的应用。比如，在设计一个正方形的游戏地图时，游戏开发者需要知道地图的面积来确定可以放置的障碍物和道具数量；同时，他们还需要知道地图的周长来设计玩家的移动路径和探索范围。

正方形的公式与数学文化

正方形的公式不仅在数学中有着重要的地位，还在数学文化中扮演着重要角色。自古以来，正方形就被视为一种完美的几何形状，它的公式也被视为数学美的体现。

在数学教育中，正方形的公式是孩子们接触几何图形的起点之一。通过学习正方形的公式，孩子们可以逐渐理解几何图形的性质和规律，培养空间想象能力和逻辑思维能力。

同时，正方形的公式也在数学竞赛和研究中发挥着重要作用。在数学竞赛中，正方形的公式经常被用来解决一些复杂的几何问题；在数学研究中，正方形的公式也被用来探索几何图形的更深层次性质和规律。

结语

正方形的公式虽然简单，但它们却蕴含着丰富的数学意义和实用价值。通过学习和掌握这些公式，我们可以更深入地理解正方形的性质和规律，更好地应用它们来解决实际问题。同时，正方形的公式也是我们探索数学奥秘、感受数学之美的一扇窗口。让我们在探索正方形的奇妙世界中，不断发现数学的魅力和力量吧！