掌握解方程的实用方法与技巧

在数学学习的征途中，解方程无疑是一座重要的里程碑。它不仅是连接代数与几何、解决实际问题的桥梁，更是培养逻辑思维和抽象能力的关键步骤。解方程的方法多种多样，每一种都蕴含着独特的数学智慧。本文将从基础概念、常见类型、解题策略、技巧提升以及实际应用等多个维度，深入探讨如何有效地解方程。

一、基础概念：方程与解的定义

方程，简而言之，是含有未知数的等式。未知数通常用字母（如x、y）表示，而等式则表明两边的数值或表达式相等。解方程，即找出使等式成立的未知数的值，这个值被称为方程的解或根。

二、常见类型：一元一次到高次方程的演变

1. 一元一次方程

一元一次方程是最简单的方程形式，形如ax+b=c（a≠0）。解这类方程，只需将含未知数的项移至等式一侧，常数项移至另一侧，然后除以未知数的系数即可。例如，解方程3x+5=14，先移项得3x=9，再除以3得x=3。

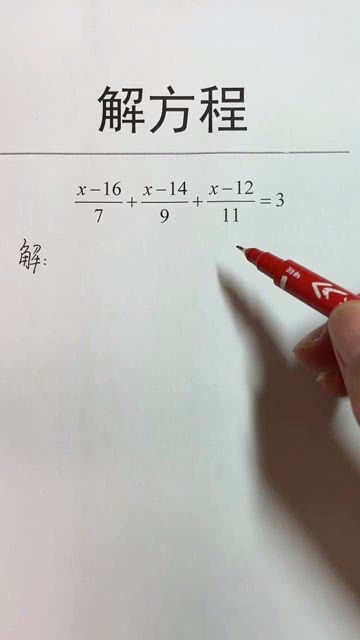
2. 一元二次方程

一元二次方程形如ax²+bx+c=0（a≠0），其解法包括公式法和因式分解法。公式法依赖于求根公式x=[-b±√(b²-4ac)]/2a，适用于所有一元二次方程；而因式分解法则要求方程能分解为两个一次因式的乘积，如x²-5x+6=(x-2)(x-3)=0，直接得出解x=2或x=3。

3. 高次方程

对于三次及以上的一元方程，求解过程通常更为复杂，可能涉及卡尔丹公式、数值方法或特殊技巧。在实际应用中，高次方程往往通过换元法、降次法等转化为低次方程求解。

三、解题策略：逻辑与直觉并重

1. 识别方程类型

面对一个方程，首要任务是识别其类型，这决定了后续采用的解题策略。例如，识别出一元二次方程后，应立即考虑是否适用因式分解法或求根公式。

2. 简化方程

简化方程是解题的关键步骤，包括合并同类项、移项、消去分母等。简化后的方程往往更易于求解。

3. 逆向思维

逆向思维在解方程中尤为重要。例如，在解一元一次方程时，逆向操作（如减法变加法、除法变乘法）是求解的关键。

4. 验证解的正确性

求得解后，务必将其代入原方程验证，确保等式成立。这是检验解题过程正确性的有效手段。

四、技巧提升：从基础到进阶

1. 熟练掌握基本运算

解方程的基础是熟练掌握加减乘除、平方根等基本运算。只有在此基础上，才能快速准确地执行移项、合并同类项等操作。

2. 灵活运用公式与定理

对于一元二次方程，熟练掌握求根公式和判别式Δ=b²-4ac的意义至关重要。此外，了解韦达定理（根与系数的关系）也能在特定情境下简化解题过程。

3. 培养直觉与洞察力

解方程不仅是机械地应用公式，更需培养对问题的直觉和洞察力。通过观察方程的结构，有时能迅速找到解题的突破口。

4. 尝试多种解法

对于同一方程，尝试不同的解法不仅能锻炼思维灵活性，还能在比较中发现最优解。例如，对于某些一元二次方程，因式分解可能比使用求根公式更直观快捷。

五、实际应用：方程与生活的紧密联系

解方程不仅是数学课堂上的练习，更是解决现实问题的有力工具。从物理学的运动方程到经济学的供需平衡，从工程学的结构设计到生物学的种群增长模型，方程无处不在。

1. 物理学中的应用

在物理学中，解方程常用于描述物体的运动状态，如自由落体运动中的位移-时间方程、牛顿第二定律中的加速度-力方程等。

2. 经济学中的应用

经济学中，供需平衡模型、成本收益分析等常涉及方程求解。例如，通过设立并解决供需方程，可以预测市场价格的变化趋势。

3. 工程学中的应用

在工程设计中，结构稳定性分析、材料强度计算等都需要建立并解决复杂的方程组。方程的解直接决定了设计的可行性和安全性。

4. 生物学中的应用

生物学中，种群增长模型（如Logistic模型）通过解方程预测物种数量的变化趋势，对生态保护、资源管理具有重要意义。

结语

解方程，作为数学学习的核心内容之一，不仅锻炼了我们的逻辑思维和计算能力，更让我们学会了如何将抽象知识应用于解决实际问题。从一元一次方程到高次方程，从基础运算到公式定理的灵活运用，每一步都充满了挑战与乐趣。在这个过程中，我们学会了观察、思考、尝试与验证，这些能力将伴随我们一生，成为我们探索未知世界的宝贵财富。因此，让我们珍惜每一次解方程的机会，用心去感受数学的魅力，用智慧去解锁世界的奥秘。