如何判定平行线的五种方法？

平行线，作为几何学中的一个基本概念，是指在同一平面内，永不相交的两条直线。理解平行线的判定方法，对于掌握平面几何的基础知识至关重要。以下是平行线的五种主要判定方法，通过简明扼要的介绍，旨在帮助读者更好地理解和应用这些判定定理。

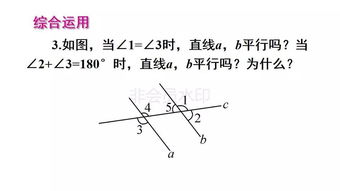
第一种方法：同位角相等，两直线平行

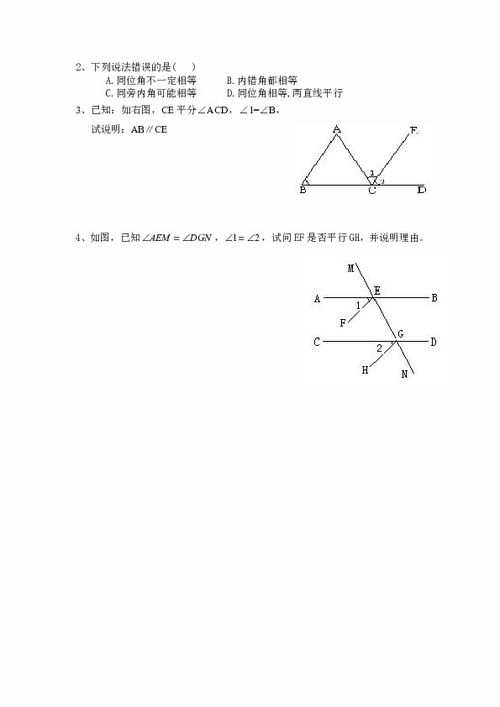
同位角相等是两直线平行的最常用判定方法之一。当两条直线被第三条直线（称为截线）所截，如果它们在截线的同一侧且位于被截两直线的同一方向（即同位）的两个角相等，则这两条直线平行。这种判定方法可以用几何符号表示为：如果∠1=∠2，则AB∥CD，其中∠1和∠2为同位角，AB和CD为被截的两直线。

第二种方法：内错角相等，两直线平行

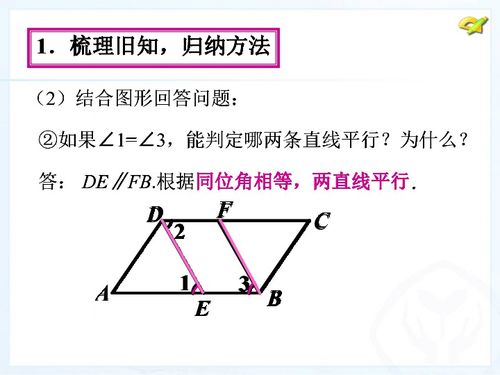
内错角相等是另一种常用的平行线判定方法。当两条直线被第三条直线所截，如果它们在截线的两侧且一个角位于被截两直线之一的内部，另一个角位于该直线的外部（即内错），且这两个角相等，则这两条直线平行。同样地，这种判定方法可以用几何符号表示为：如果∠1=∠3，则AB∥CD，其中∠1和∠3为内错角，AB和CD为被截的两直线。

第三种方法：同旁内角互补，两直线平行

同旁内角互补是两直线平行的第三种判定方法。当两条直线被第三条直线所截，如果它们在截线的同一侧且位于被截两直线的内部（即同旁内），且这两个角的度数之和为180°（即互补），则这两条直线平行。用几何符号表示即：如果∠1+∠2=180°，则AB∥CD，其中∠1和∠2为同旁内角，AB和CD为被截的两直线。

第四种方法：平行于同一条直线的两直线平行

这一判定方法，也被称为平行线的传递性，指的是如果两条直线都平行于第三条直线，那么这两条直线也互相平行。这个定理在实际应用中非常有用，因为它允许我们通过已知的一条平行线来推断其他直线的平行性。例如，如果AB∥EF且EF∥CD，则可以推断出AB∥CD。

第五种方法：根据平行线的定义

平行线的定义本身也可以作为一种判定方法。在同一平面内，如果两条直线不相交，则它们互相平行。这个定义是最基本的，也是其他判定方法的基础。然而，在实际应用中，我们通常更倾向于使用前四种更为具体的判定方法，因为定义本身并没有提供足够的判定依据，而是更多地作为平行线概念的基础。

平行线判定方法的深入理解和应用

要深入理解平行线的判定方法，并将其灵活应用于实际解题中，需要注意以下几点：

1. 理解角的概念和性质：

同位角、内错角、同旁内角是判定平行线的基础，因此必须准确理解这些角的定义和性质。在几何图形中，通过识别这些角，可以方便地应用判定方法。

2. 掌握几何符号的使用：

几何符号是表示几何图形和关系的重要工具。掌握几何符号的使用，可以简洁明了地表示和证明平行线的判定过程。

3. 灵活运用判定方法：

在实际应用中，需要根据题目的具体情况，灵活运用不同的判定方法。有时需要综合运用多种方法，才能得出正确的结论。

4. 注意平行线的传递性：

平行线的传递性是判定平行线的一个重要性质。在解题过程中，可以利用这一性质来简化证明过程。

5. 理解平行线的性质：

平行线的性质是判定方法的逆命题，即如果两条直线平行，则它们之间的同位角、内错角、同旁内角分别相等或互补。理解这些性质有助于加深对平行线判定方法的理解和应用。

平行线判定方法的实际应用案例

以下是一个关于平行线判定方法的实际应用案例：

题目：

已知在四边形ABCD中，∠A+∠C=180°，∠B+∠D=180°，求证：AB∥CD，AD∥BC。

证明：

第一步，根据同旁内角互补的性质，我们知道如果两条直线被第三条直线所截，且同旁内角互补，则这两条直线平行。

第二步，根据题目条件，∠A和∠C是同旁内角，且∠A+∠C=180°，所以AB∥CD。

第三步，同样地，∠B和∠D也是同旁内角，且∠B+∠D=180°，所以AD∥BC。

综上所述，我们证明了AB∥CD，AD�