空间向量平行与垂直的公式是什么

空间向量，作为数学和物理学中的重要概念，描述了空间中具有大小和方向的量。当我们深入探索这些向量的关系时，会发现平行和垂直是两种基本的向量关系。理解这两种关系的关键在于掌握空间向量的平行公式和垂直公式。

首先，让我们从平行向量的概念开始。平行向量，也被称为共线向量，是指方向相同或相反的向量。在二维平面或三维空间中，平行向量之间的关系可以通过一个简单的数学表达式来描述：若向量a与向量b平行，则存在一个非零实数k，使得向量a等于k乘以向量b，即a=k*b。这个公式揭示了平行向量的本质，即它们之间的比例关系。换句话说，无论向量a和向量b的模（或长度）如何，只要它们的方向相同或相反，并且满足上述比例关系，那么我们就可以说它们是平行的。

以具体的向量为例，假设向量a=(a1,a2)，向量b=(b1,b2)，如果a与b平行，那么它们的坐标将满足a1/b1=a2/b2（假设b1和b2均不为0，以避免除以0的情况）。这个比例关系也可以表示为a1*b2=a2*b1，或者更一般地，a=λb，其中λ是一个常数（在这个上下文中，λ实际上就是k的另一种表示方式）。这些表达式都是平行向量公式的不同形式，它们在数学和物理学中都有着广泛的应用。

接下来，我们转向垂直向量的概念。垂直向量是指方向相互垂直的向量。在二维平面或三维空间中，两个向量垂直的充要条件是它们的点积为0。点积是一种衡量两个向量之间“夹角”的度量方式，当两向量垂直时，它们之间的夹角为90度，此时点积为0。具体来说，如果向量a=(x1,y1)，向量b=(x2,y2)，那么a与b垂直的充要条件是x1*x2+y1*y2=0。这个公式是垂直向量公式的核心，它为我们提供了一种判断两个向量是否垂直的简便方法。

值得注意的是，垂直向量的公式在二维和三维空间中都是适用的。在二维空间中，我们可以将向量的坐标看作是在平面直角坐标系中的点，而垂直关系则对应于这些点之间的垂直线段。在三维空间中，向量的坐标则是在空间直角坐标系中的点，而垂直关系则对应于这些点之间的垂直平面或垂直线段。无论在哪种情况下，只要满足垂直向量的公式，我们就可以确定两个向量是垂直的。

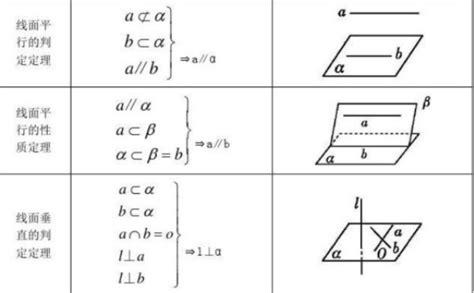
平行向量和垂直向量的公式在解决实际问题中有着广泛的应用。例如，在物理学中，力、速度和加速度等物理量都可以表示为向量。当我们需要判断这些物理量之间的方向关系时，就可以利用平行向量和垂直向量的公式来进行计算。此外，在工程学中，向量的概念也被广泛应用于结构分析、力学计算等领域。在这些领域中，平行向量和垂直向量的公式为我们提供了一种强大的工具，用于分析和解决复杂的问题。

除了上述应用之外，平行向量和垂直向量的公式还在几何学中发挥着重要作用。在几何学中，向量被用来描述点、线、面等几何元素之间的关系。通过利用平行向量和垂直向量的公式，我们可以判断几何元素之间的平行和垂直关系，从而进一步推导出它们的性质和定理。例如，在平面几何中，我们可以利用平行向量的公式来证明平行线的性质；在立体几何中，我们可以利用垂直向量的公式来证明垂直平面的性质。

此外，平行向量和垂直向量的公式还与向量的线性组合、向量的投影等概念密切相关。线性组合是指将一组向量按照一定的系数进行加法和数乘运算后得到的新的向量。在这个过程中，平行向量的公式可以帮助我们判断哪些向量可以构成线性组合，以及这些线性组合的性质。而向量的投影则是指将一个向量在另一个向量方向上的投影长度。在这个过程中，垂直向量的公式可以帮助我们判断哪些向量是垂直的，从而确定投影的长度和方向。

总之，空间向量的平行公式和垂直公式是数学和物理学中的重要工具。它们为我们提供了一种描述和判断向量之间关系的方法，使我们能够更深入地理解和应用向量的概念。通过掌握这些公式，我们可以更好地解决实际问题，推动科学技术的发展。

为了加深对这两个公式的理解，我们可以通过一些具体的例子来进行练习。例如，给定两个向量a=(1,2)和b=(2,4)，我们可以利用平行向量的公式来判断它们是否平行。在这个例子中，我们可以看到a的坐标与b的坐标之间满足比例关系，即1/2=2/4，因此我们可以确定a与b是平行的。同样地，给定两个向量c=(1,1)和d=(-1,1)，我们可以利用垂直向量的公式来判断它们是否垂直。在这个例子中，我们可以看到c和d的坐标满足垂直向量的公式，即1*(-1)+1*1=0，因此我们可以确定c与