二进制转换到十进制的方法

二进制转十进制全攻略

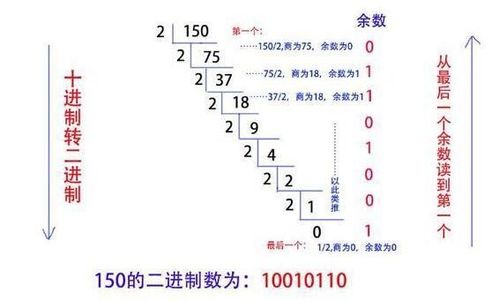
在计算机科学和数字电子领域，二进制和十进制是两种最常见的数制。二进制只有0和1两个数字，是计算机内部信息处理的基础；而十进制则是我们日常生活中广泛使用的数制，包括0到9十个数字。理解二进制和十进制之间的转换，对于掌握计算机的基本工作原理至关重要。本文将详细介绍二进制转十进制的方法，并通过实例展示转换过程。

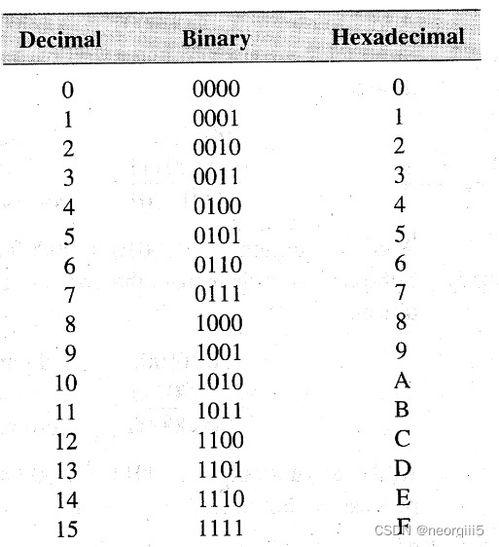
一、二进制与十进制的基本概念

二进制（Binary）：二进制是一种基于2的数制，用0和1两个数字表示数值。在计算机科学中，二进制是数据存储和处理的基础。每个二进制位（bit）只能是0或1，多个二进制位组合在一起可以表示更大的数值。

十进制（Decimal）：十进制是我们日常生活中使用的数制，基于10，用0到9十个数字表示数值。十进制数可以通过位权（或称权值）来表示，例如，在十进制数123中，1的位权是100（10^2），2的位权是10（10^1），3的位权是1（10^0）。

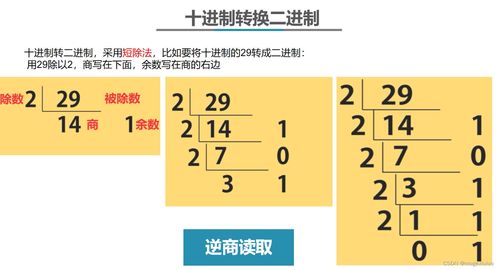
二、二进制转十进制的方法

二进制转十进制的过程相对简单，就是将二进制数中的每一位乘以对应的位权（2的幂次方），然后将所有结果相加。具体步骤如下：

1. 确定二进制数的位数：首先，确定二进制数的位数，从右往左数，最右边的位是第0位，依次向左递增。

2. 计算每一位的位权：根据二进制数的位数，计算每一位对应的位权。位权是2的幂次方，从右往左依次为2^0、2^1、2^2、...、2^(n-1)，其中n是二进制数的位数。

3. 将每一位与位权相乘：将二进制数中的每一位与对应的位权相乘，得到该位的十进制值。

4. 将所有结果相加：将上一步得到的所有十进制值相加，得到最终的十进制数。

三、实例演示

实例1：二进制数101转换为十进制数

1. 确定二进制数的位数：二进制数101有3位。

2. 计算每一位的位权：

第0位的位权是2^0 = 1

第1位的位权是2^1 = 2

第2位的位权是2^2 = 4

3. 将每一位与位权相乘：

第0位（最右边）是1，与位权1相乘，得到1 * 1 = 1

第1位是0，与位权2相乘，得到0 * 2 = 0

第2位（最左边）是1，与位权4相乘，得到1 * 4 = 4

4. 将所有结果相加：1 + 0 + 4 = 5

因此，二进制数101转换为十进制数是5。

实例2：二进制数1101转换为十进制数

1. 确定二进制数的位数：二进制数1101有4位。

2. 计算每一位的位权：

第0位的位权是2^0 = 1

第1位的位权是2^1 = 2

第2位的位权是2^2 = 4

第3位的位权是2^3 = 8

3. 将每一位与位权相乘：

第0位是1，与位权1相乘，得到1 * 1 = 1

第1位是0，与位权2相乘，得到0 * 2 = 0

第2位是1，与位权4相乘，得到1 * 4 = 4

第3位是1，与位权8相乘，得到1 * 8 = 8

4. 将所有结果相加：1 + 0 + 4 + 8 = 13

因此，二进制数1101转换为十进制数是13。

实例3：二进制数10101转换为十进制数

1. 确定二进制数的位数：二进制数10101有5位。

2. 计算每一位的位权：

第0位的位权是2^0 = 1

第1位的位权是2^1 = 2

第2位的位权是2^2 = 4

第3位的位权是2^3 = 8

第4位的位权