二进制转十进制的方法

二进制如何转化为十进制？一篇让你秒懂的科普文

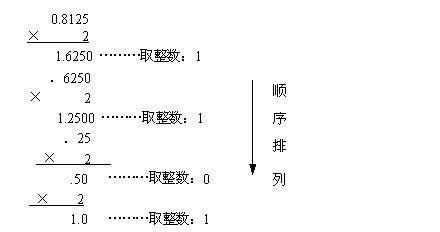
在数字化时代，我们每天都与计算机、智能手机、网络等数字设备打交道。然而，你是否曾经想过，这些设备内部是如何处理信息的呢？其实，它们都依赖于一种非常基础的数学体系——二进制。那么，二进制是什么？它又是如何转化为我们熟悉的十进制数的呢？接下来，就让我们一起揭开这个神秘的面纱吧！

一、二进制初印象：数字世界的“0”和“1”

首先，我们来了解一下二进制的基本概念。二进制，顾名思义，就是只有两种状态的计数系统，这两种状态分别用“0”和“1”来表示。与我们平时使用的十进制相比，二进制显得非常简洁和直观。在十进制中，我们使用0到9这十个数字来表示数值，而在二进制中，我们只需要“0”和“1”这两个数字就足够了。

为什么计算机要使用二进制呢？这主要是因为二进制非常适合计算机内部的逻辑运算和存储。计算机内部的电路只有开（ON）和关（OFF）两种状态，这与二进制的“0”和“1”完美对应。此外，二进制还具有抗干扰能力强、运算规则简单等优点，使得计算机能够高效、准确地处理信息。

二、二进制与十进制的桥梁：位权与加权求和

了解了二进制的基本概念后，我们来看看如何将二进制数转化为十进制数。这个过程其实并不复杂，关键在于理解“位权”和“加权求和”的概念。

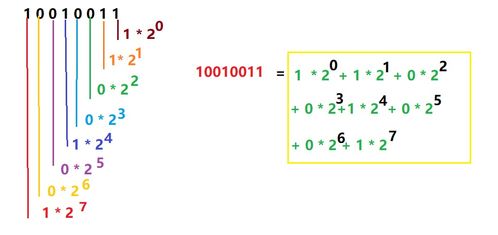
位权，简单来说，就是二进制数中每一位所代表的权重。在二进制中，从右往左数，第一位（最右边）的位权是2的0次方，第二位是2的1次方，第三位是2的2次方，以此类推。例如，在二进制数“101”中，从右往左数，第一位（最右边的“1”）的位权是2的0次方（即1），第二位（中间的“0”）的位权是2的1次方（即2），第三位（最左边的“1”）的位权是2的2次方（即4）。

加权求和，就是将二进制数中每一位的数值与其对应的位权相乘，然后将得到的乘积相加。这样，我们就可以得到该二进制数对应的十进制数了。例如，在二进制数“101”中，最右边的“1”对应的十进制数是1（因为1乘以2的0次方等于1），中间的“0”对应的十进制数是0（因为0乘以2的1次方等于0），最左边的“1”对应的十进制数是4（因为1乘以2的2次方等于4）。因此，二进制数“101”对应的十进制数就是1+0+4=5。

三、实战演练：二进制转化为十进制

了解了二进制转化为十进制的基本原理后，我们来通过几个实例进行实战演练。

实例一：二进制数“1101”转化为十进制数

首先，我们确定二进制数“1101”中每一位的位权：

第一位（最右边的“1”）的位权是2的0次方，即1；

第二位（右边的“0”）的位权是2的1次方，即2；

第三位（中间的“1”）的位权是2的2次方，即4；

第四位（最左边的“1”）的位权是2的3次方，即8。

然后，我们将每一位的数值与其对应的位权相乘，并将得到的乘积相加：

第一位（最右边的“1”）对应的十进制数是1（因为1乘以2的0次方等于1）；

第二位（右边的“0”）对应的十进制数是0（因为0乘以2的1次方等于0）；

第三位（中间的“1”）对应的十进制数是4（因为1乘以2的2次方等于4）；

第四位（最左边的“1”）对应的十进制数是8（因为1乘以2的3次方等于8）。

因此，二进制数“1101”对应的十进制数就是1+0+4+8=13。

实例二：二进制数“101010”转化为十进制数

同样地，我们首先确定二进制数“101010”中每一位的位权：

第一位（最右边的“0”）的位权是2的0次方，即1；

第二位（右边的“1”）的位权是2的1次方，即2；

第三位（中间的“0”）的位权是2的2次方，即4；

第四位（左边的“1”）的位权是2的3次方，即8；

第五位（再左边的“0”）的位权是2的4次方，即16；

第六位（最左边的“1”）的