两个向量相乘的计算方法是什么？

在数学的广阔天地里，向量作为一个基础而强大的工具，其应用无处不在，从物理学中的力与速度，到计算机图形学中的变换与渲染，再到经济学中的多元分析与预测，向量都扮演着举足轻重的角色。而向量的乘法，则是解锁这些应用的关键之一。本文将多维度地探讨两个向量相乘的计算方法，包括数量积（点积）、向量积（叉积）以及矩阵乘法中的向量乘法，旨在为读者提供一个全面而深入的理解。

数量积：几何与代数的桥梁

数量积，又称点积，是两个向量间最直观的一种乘法形式。其计算公式为：

\[a \cdot b = |a| \times |b| \times \cos \theta\]

其中，\(a\) 和 \(b\) 是两个向量，\(|a|\) 和 \(|b|\) 分别表示它们的模（即长度），\(\theta\) 是它们之间的夹角。从这个公式可以看出，点积的结果是一个标量（实数），它反映了两个向量在方向和大小上的“兼容性”。

从几何意义上讲，点积等于一个向量在另一个向量方向上的投影长度乘以另一个向量的模。这解释了为什么当两向量垂直时（夹角为90度），它们的点积为零——因为一个向量在另一个垂直方向上的投影长度为零。

代数上，如果向量 \(a = (a_1, a_2, ..., a_n)\) 和 \(b = (b_1, b_2, ..., b_n)\)，则它们的点积可以表示为：

\[a \cdot b = a_1b_1 + a_2b_2 + ... + a_nb_n\]

这种计算方式简洁明了，非常适合于计算机编程中的快速计算。点积的应用广泛，比如计算两向量之间的夹角、判断两向量的相似性或正交性、以及在物理学中计算功等。

向量积：三维空间中的独特存在

向量积，又称叉积，是仅限于三维向量的一种特殊乘法。其结果是一个向量，而非标量，这个新向量垂直于原两个向量所构成的平面。向量积的公式为：

\[c = a \times b\]

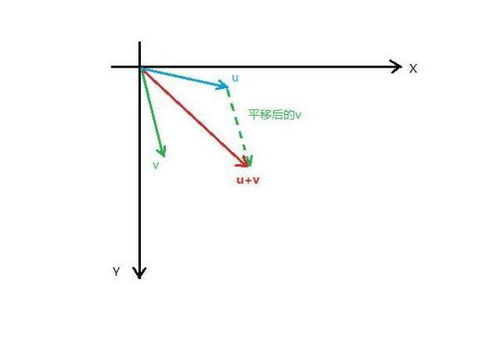
其中，\(c\) 是新生成的向量，其模等于原两向量模的乘积与它们之间夹角的正弦值的乘积，方向遵守右手定则。具体来说，如果将右手四指从向量 \(a\) 指向向量 \(b\)，则大拇指的方向即为向量积 \(c\) 的方向。

向量积的计算公式稍显复杂，对于三维向量 \(a = (a_1, a_2, a_3)\) 和 \(b = (b_1, b_2, b_3)\)，它们的向量积 \(c = (c_1, c_2, c_3)\) 可以通过行列式来求解：

\[c = \begin{vmatrix}

\mathbf{i} & \mathbf{j} & \mathbf{k} \\

a_1 & a_2 & a_3 \\

b_1 & b_2 & b_3

\end{vmatrix}\]

展开后得到：

\[c_1 = a_2b_3 - a_3b_2\]

\[c_2 = a_3b_1 - a_1b_3\]

\[c_3 = a_1b_2 - a_2b_1\]

向量积在物理学和工程学中有着重要应用，如计算力矩、磁场力、以及判断平面的法向量等。此外，它还是三维图形学中计算表面法线和光照效果的基础。

矩阵乘法中的向量乘法

除了上述两种基本的向量乘法外，向量还可以通过矩阵乘法与矩阵或另一个向量相互作用。这种乘法形式更加灵活，广泛应用于线性代数、计算机图形学、机器学习等领域。

向量与矩阵的乘法

当一个向量（通常表示为列向量）与一个矩阵相乘时，结果是一个新的向量。这种乘法遵循矩阵乘法的规则，即向量的每个分量分别与矩阵的对应行相乘后求和，形成新向量的一个分量。

设向量 \(v = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}\) 和矩阵 \(A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}\)，则 \(Av\) 的第 \(i\) 个分量计算如下：

\[(Av)_i