如何求解平面的法向量

时间：2024-11-11 来源：未知作者：佚名

平面的法向量是空间解析几何中的一个重要概念，它指的是与平面垂直的非零向量。在几何学、计算机图形学、机械设计等领域，平面的法向量有着广泛的应用。掌握平面的法向量的计算方法，对于解决实际问题至关重要。本文将详细介绍三种求平面法向量的方法：通过三个点、平面方程以及两个向量。

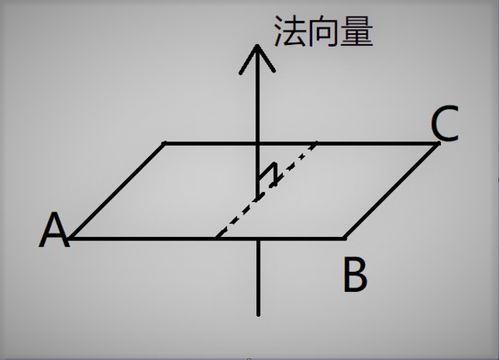
如何求解平面的法向量 1

通过三个点求平面的法向量

当我们有三个在空间上不共线的点P1(x1, y1, z1)、P2(x2, y2, z2)和P3(x3, y3, z3)时，这三个点可以确定一个平面。平面的法向量n = (n1, n2, n3)可以通过以下公式计算：

如何求解平面的法向量 2

如何求解平面的法向量 3

\mathbf{n} = \left( (y_2 - y_1)(z_3 - z_1) - (z_2 - z_1)(y_3 - y_1), \, (z_2 - z_1)(x_3 - x_1) - (x_2 - x_1)(z_3 - z_1), \, (x_2 - x_1)(y_3 - y_1) - (y_2 - y_1)(x_3 - x_1) \right)

如何求解平面的法向量 4

这个公式表明，法向量的三个分量分别由三个点的坐标计算得到。具体步骤如下：

1. 计算两个向量的差：

\overrightarrow{P1P2} = (x_2 - x_1, y_2 - y_1, z_2 - z_1)

\overrightarrow{P1P3} = (x_3 - x_1, y_3 - y_1, z_3 - z_1)

2. 使用向量的叉积公式计算法向量：

\mathbf{n} = \overrightarrow{P1P2} \times \overrightarrow{P1P3}

通过上述方法，我们可以很容易地求出平面的法向量。

通过平面方程求平面的法向量

如果已知一个平面的方程Ax + By + Cz + D = 0，那么平面的法向量就是(A, B, C)。这是因为平面方程的系数A、B、C就是法向量的三个分量。这种方法非常直接，只要知道平面的方程，就可以直接得到法向量。

例如，对于平面方程2x - 3y + 4z - 5 = 0，法向量为(2, -3, 4)。

通过两个向量求平面的法向量

有时候，我们可能知道平面上的两个不平行的向量v1和v2。在这种情况下，平面的法向量可以通过这两个向量的叉积来计算，即：

\mathbf{n} = \mathbf{v1} \times \mathbf{v2} = (v1_y \cdot v2_z - v1_z \cdot v2_y, \, v1_z \cdot v2_x - v1_x \cdot v2_z, \, v1_x \cdot v2_y - v1_y \cdot v2_x)

这个公式表明，法向量的三个分量分别由两个向量的分量计算得到。具体步骤如下：

1. 假设已知向量v1 = (v1_x, v1_y, v1_z)和v2 = (v2_x, v2_y, v2_z)。

2. 使用向量的叉积公式计算法向量：

\mathbf{n} = (v1_y \cdot v2_z - v1_z \cdot v2_y, \, v1_z \cdot v2_x - v1_x \cdot v2_z, \, v1_x \cdot v2_y - v1_y \cdot v2_x)

通过上述方法，我们也可以求出平面的法向量。