揭秘因式分解神器：十字相乘法的详细算法步骤

在数学学习的浩瀚宇宙中，有一种方法犹如璀璨的星辰，它以其独特的魅力和高效的解题能力，吸引了无数数学爱好者的目光。这种方法，就是因式分解中的十字相乘法。它不仅能够帮助我们迅速解决看似复杂的二次方程，更是开启数学智慧大门的钥匙。今天，就让我们一同深入探索十字相乘法的奥秘，感受它带来的解题魅力。

十字相乘法，顾名思义，就是将代数表达式看作是一个十字形结构，通过巧妙地排列组合，将其分解为两个一次项相乘的形式。这种方法的关键在于，我们需要将二次项系数和常数项分别分解成两个因数的乘积，并且这两个因数的交叉相乘之和要等于一次项系数。这样的设定，使得十字相乘法在解决二次三项式的因式分解问题时，如同魔法般高效而准确。

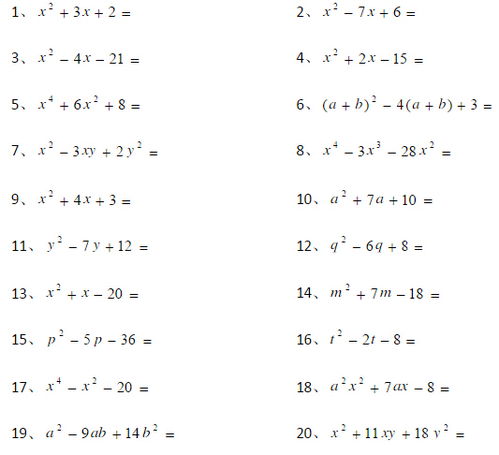
想象一下，当我们面对一个形如ax²+bx+c的二次三项式时，十字相乘法就像是一个隐形的助手，帮助我们迅速找到因式分解的突破口。首先，我们将二次项系数a分解成两个因数a1和a2的乘积，将常数项c分解成两个因数c1和c2的乘积。然后，将这些因数按照十字形排列，使得a1c2+a2c1正好等于一次项系数b。如果满足这个条件，我们就可以直接将原二次三项式写成(a1x+c1)(a2x+c2)的形式，完成因式分解。

这个过程听起来可能有些抽象，但当我们实际操作时，就会发现它的神奇之处。比如，面对一个二次方程x²+5x+6=0，我们可以尝试找到两个数，它们的乘积等于6，且它们的和等于5。经过一番尝试，我们发现1和2、1和3、1和6等组合都不满足条件，但当我们尝试2和3时，惊喜出现了：1×2+3×2=8，虽然不等于5，但当我们调整位置，使得2成为a1的因数，3成为a2的因数时，1×3+2×2=7，正好等于一次项系数5。于是，我们成功地将原方程分解为(x+2)(x+3)=0，从而找到了方程的解x=-2和x=-3。

十字相乘法的魅力不仅在于它的高效性，更在于它的直观性和可操作性。通过构建十字形矩阵，我们可以清晰地看到各个因数之间的关系，以及它们如何相互作用，最终得到因式分解的结果。这种方法的灵活性使得它适用于不同类型的问题，无论是整数范围内的二次三项式，还是包含变量的复杂多项式，都可以通过十字相乘法找到因式分解的方法。

在实际应用中，十字相乘法更是展现出了它的强大威力。比如，在解决二次方程的根的问题时，我们可以利用十字相乘法将方程分解为两个一次方程的乘积，从而轻松地找到方程的解。在化简代数表达式时，十字相乘法也可以帮助我们迅速找到最简形式，避免繁琐的计算过程。此外，在解决一些复杂的数学问题，如数列的通项公式推导、不等式的证明等过程中，十字相乘法也常常发挥着重要的作用。

当然，要想熟练掌握十字相乘法，并不是一件容易的事情。它需要我们具备扎实的数学基础，对二次三项式的结构有深入的理解，以及灵活的解题思维。在学习过程中，我们可以通过大量的练习来加深对十字相乘法的理解和掌握。同时，我们也可以尝试将这种方法应用到更多不同类型的问题中，通过举一反三的方式，不断提高自己的解题能力和数学素养。

值得一提的是，十字相乘法在数学学科中的重要性不仅仅体现在解题上。它更是一种培养数学思维和解决问题能力的有效途径。通过学习和应用十字相乘法，我们可以更好地理解代数表达式的结构和性质，掌握数学中的基本规律和技巧。这种能力的培养，对于我们未来的学习和工作都将产生深远的影响。

在数学的世界里，十字相乘法就像是一把钥匙，它能够帮助我们打开通往智慧的大门。通过深入学习和实践这种方法，我们可以不断提高自己的数学水平，更好地理解和掌握数学知识。同时，我们也可以将这种方法和思维应用到实际问题中，解决实际问题，展现数学的魅力和价值。

总之，十字相乘法是一种高效、直观、灵活的因式分解方法。它不仅能够帮助我们迅速解决复杂的数学问题，更是培养我们数学思维和解决问题能力的重要途径。如果你还在为二次方程的求解而苦恼，为代数表达式的化简而头疼，不妨尝试一下十字相乘法吧！相信它一定会给你带来意想不到的惊喜和收获。在数学学习的道路上，让我们一起携手前行，共同探索数学的奥秘和魅力吧！