深入了解交集、并集与补集的概念

在数学的广阔领域中，集合论作为基础而强大的工具，为我们提供了理解和操作对象的强大框架。其中，交集、并集和补集是集合论中的核心概念，它们不仅是理解复杂集合关系的基石，也是解决各类实际问题的重要工具。本文将深入探讨这三个概念，通过不同的维度来揭示它们的本质和应用。

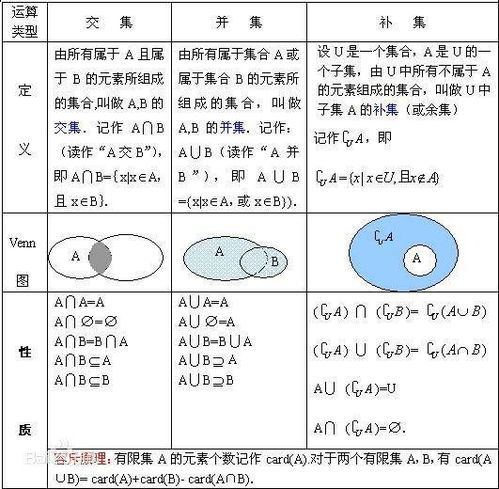
一、交集：探寻共同之处

交集，简而言之，是两个或多个集合中共有的元素组成的集合。用符号表示为：如果A和B是两个集合，那么A与B的交集记作A∩B，它包含了所有同时属于A和B的元素。交集的概念基于“共同拥有”的理念，它帮助我们从不同集合中抽取出共同的元素，从而揭示出集合之间的内在联系。

1. 直观理解

想象一个教室里有两组学生，一组是喜欢数学的学生（集合A），另一组是喜欢物理的学生（集合B）。那么，同时喜欢数学和物理的学生就构成了这两个集合的交集A∩B。这个交集告诉我们，哪些学生对这两门学科都有兴趣。

2. 数学性质

交集运算满足一些重要的性质，如交换律（A∩B=B∩A）、结合律（A∩(B∩C)=(A∩B)∩C）以及分配律（A∩(B∪C)=(A∩B)∪(A∩C)），这些性质使得交集在复杂的集合运算中保持了一致性和可预测性。

3. 应用实例

在数据分析中，交集可以用来找出两个数据集中共有的记录，比如找出同时购买某两种产品的顾客名单。在社交网络中，交集可以帮助我们识别共同关注的话题或人物，从而加深用户之间的联系。

二、并集：融合多元视角

与交集相对，并集关注的是将两个或多个集合中的所有元素合并起来，形成一个新的集合。用符号表示为：如果A和B是两个集合，那么A与B的并集记作A∪B，它包含了所有属于A或B（或两者都属于）的元素。并集体现了“汇总”的思想，它允许我们从不同的集合中收集信息，形成一个更全面的视角。

1. 直观理解

回到教室的例子，如果我们将喜欢数学的学生（集合A）和喜欢物理的学生（集合B）视为两个独立的群体，那么喜欢数学或物理（或两者都喜欢）的学生就构成了这两个集合的并集A∪B。这个并集涵盖了所有对数学或物理有兴趣的学生，无论他们是否同时喜欢两门学科。

2. 数学性质

并集运算同样满足交换律（A∪B=B∪A）和结合律（A∪(B∪C)=(A∪B)∪C），但不同于交集，并集不满足分配律对于集合的差集而言（即(A∪B)−C不等于(A−C)∪(B−C)）。这些性质为我们在处理集合的并集时提供了有用的指导。

3. 应用实例

在市场营销中，并集可以用来整合不同渠道的潜在客户名单，以扩大营销活动的覆盖面。在生物信息学中，并集可以帮助研究人员从多个数据库中收集基因表达数据，以进行综合分析。

三、补集：定义相对存在

补集的概念则更加侧重于描述一个集合相对于其全集（或某个更大的集合）中不属于该集合的元素组成的集合。用符号表示为：如果U是全集，A是U的一个子集，那么A在U中的补集记作A'，它包含了U中所有不属于A的元素。补集体现了“相对性”的思维，它让我们能够从一个更广阔的背景中识别出不属于特定集合的元素。

1. 直观理解

假设全集U是班级里所有学生的名单，而A是班级里喜欢打篮球的学生的名单。那么，A的补集A'就是班级里不喜欢打篮球的学生的名单。补集A'定义了那些不属于A（即不喜欢打篮球）的学生的集合。

2. 数学性质

补集运算有其独特的性质，如补集的补集等于原集合（A''=A），以及德摩根定律（(A∩B)'=A'∪B'和(A∪B)'=A'∩B'），这些性质在逻辑推理和集合运算中起着至关重要的作用。

3. 应用实例

在数据库管理中，补集可以用来找出缺失的数据，比如找出某个数据库中未记录的客户信息。在网络安全中，补集可以帮助识别未被防火墙规则覆盖的潜在漏洞，从而增强系统的安全性。

四、交集、并