开普勒第二定律的证明方法

如何证明开普勒第二定律

开普勒第二定律，也被称为面积定律，是天体力学中的一条基本定律。该定律指出，对于同一个行星而言，在相等的时间内扫过的面积相等。这意味着行星在绕太阳运动时，与太阳连线所扫过的面积速度是恒定的。

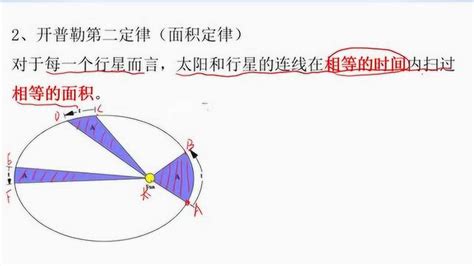
为了证明开普勒第二定律，我们可以从行星的运动方程出发，结合向心力和角动量守恒的原理进行推导。以下是一个详细的证明过程：

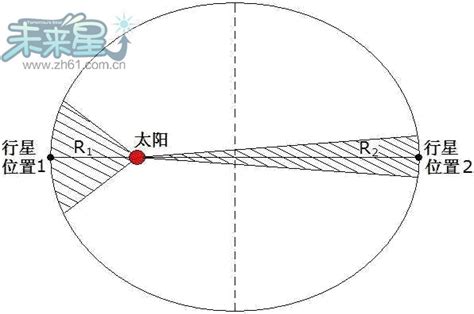
首先，我们考虑行星绕太阳做椭圆轨道运动的情况。在椭圆轨道上，行星与太阳的距离r会随时间变化，但我们可以根据开普勒第一定律（椭圆轨道定律）知道，行星始终位于一个椭圆轨道上，太阳位于椭圆的一个焦点上。

一、运动方程与向心力

行星在椭圆轨道上运动时，其运动可以分解为径向和切向两个分量。径向分量使行星沿着椭圆轨道靠近或远离太阳，而切向分量则使行星沿着轨道的切线方向运动。

根据牛顿第二定律，行星所受的向心力F等于其质量m乘以加速度a。在椭圆轨道上，向心力由太阳对行星的万有引力提供，可以表示为：

F=G(Mmsun/r^2)

其中，G是万有引力常数，Mmsun是太阳的质量，r是行星与太阳之间的距离。

二、行星的速度与角速度

设行星的速度为v，角速度为ω，则行星的线速度v可以表示为：

v=dr/dt（r为行星与太阳的距离，t为时间）

角速度ω则可以表示为行星与太阳连线转过的角度θ对时间的导数，即：

ω=dθ/dt

在极坐标系中，行星的速度v可以分解为径向速度vr和切向速度vt两个分量，其中：

vr=dr/dt

vt=r×dθ/dt=rω

三、面积扫过的速率

考虑行星在dt时间内扫过的面积ΔA，该面积可以近似为以行星与太阳连线为底，以行星在dt时间内走过的弧长为高的三角形面积。因此，有：

ΔA≈0.5×r×vt×dt=0.5×r^2×ω×dt

当dt趋近于0时，上述近似变为精确值，即行星在dt时间内扫过的面积为：

dA=0.5×r^2×ω×dt

为了证明开普勒第二定律，我们需要证明dA/dt（即面积扫过的速率）是一个常数。

四、面积扫过速率的证明

根据链式法则和行星运动方程，我们可以求出dA/dt的表达式。首先，我们有：

dA/dt=0.5×d(r^2×ω)/dt

然后，利用乘积法则进行展开：

dA/dt=0.5×(2r×dr/dt×ω+r^2×dω/dt)

接着，我们将切向速度vt和角速度ω的表达式代入上式：

dA/dt=0.5×(2r×(vt/r)×(v/r)-r^2×(v/r^2)×d(v/r)/dt)（因为ω=v/r，所以dω/dt=(dv/dt)/r-v×(dr/dt)/r^2）

化简后得到：

dA/dt=v×vt-0.5×r^2×(1/r^2)×d(v^2)/dt+0.5×r^2×(2v/r^3)×v×dr/dt

进一步化简：

dA/dt=v×vt-0.5×d(v^2)/dt+v^2×(dr/dt)/r（注意，这里dr/dt和vt在径向方向上是相反的，但在此处我们仅考虑其大小）

由于行星在椭圆轨道上运动时，其动能和势能之和保持不变（即机械能守恒），因此有：

0.5×m×v^2-G(Mmsun×m/r)=const

对上式两边关于时间t求导，得到：

m×v×dv/dt+G(Mmsun×m/r^2)×dr/dt=0

化简后得到：

v×dv/dt=-(G×Mmsun/r^2)×dr/dt

将上式代入dA/dt的表达式中，得到：

dA/dt=v×vt+0.5×m×(G×Mmsun/r^2)×(dr/dt)/m-v^2×(dr/dt)/r