区间有哪三种常见的表示方法？

在数学和日常应用中，区间是描述一系列连续数值范围的常用方式。理解并掌握区间的表示方法，不仅有助于精确地进行数学计算，还能提升我们在数据处理、统计分析等多个领域的工作效率。区间的表示方法主要分为三种：闭区间、开区间和半开半闭区间。每一种表示方法都有其独特的应用场景和数学意义，下面我们从定义、符号表示、图形化展示、实例解析及实际应用等多个维度来详细探讨这三种区间表示方法。

闭区间

定义：闭区间包含区间的两个端点。换句话说，如果区间定义为[a, b]，那么a和b都是该区间内的元素。

符号表示：闭区间使用方括号来表示，例如[a, b]。

图形化展示：在数轴上，闭区间表现为从a到b的一段连续的线段，并且a和b两点都在这条线段上。

实例解析：考虑闭区间[3, 7]，它包含所有从3到7（包括3和7）的实数。这意味着，如4、5.5、6.999...等都属于该区间。

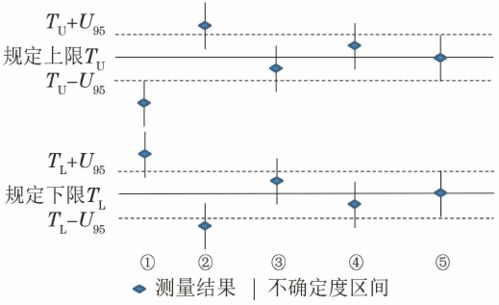
实际应用：闭区间在数学定理、物理问题中广泛出现。例如，在描述某个物体的速度在某个具体时间段内保持在某一范围内时，常用闭区间表示其速度的上下限。在统计分析中，置信区间往往也用闭区间表示，以确保数据范围内的所有可能性都被涵盖。

开区间

定义：开区间不包含区间的两个端点。若区间定义为(a, b)，则a和b均不属于该区间。

符号表示：开区间使用圆括号来表示，例如(a, b)。

图形化展示：在数轴上，开区间同样表现为从a到b的一段连续的线段，但a和b两点不在这条线段上，即线段两端是空的。

实例解析：以开区间(2, 5)为例，它包含所有大于2且小于5的实数。注意，2和5本身不属于这个区间，所以像2.0001、4.9999等数属于该区间，但2和5不属于。

实际应用：开区间在函数域分析、概率论等领域中扮演着重要角色。例如，在分析一个函数的定义域时，可能会遇到该函数仅在某一开区间内有定义的情况。在概率论中，讨论某事件的概率时，若事件发生在某个时间或数值范围内但不包括边界，此时就需要使用开区间。

半开半闭区间

定义：半开半闭区间包含区间的一个端点但不包含另一个端点。有两种形式：[a, b)和(a, b]。

符号表示：半开半闭区间使用一个方括号和一个圆括号混合表示，如[a, b)表示包含a但不包含b的区间，(a, b]则表示包含b但不包含a的区间。

图形化展示：在数轴上，半开半闭区间表现为一条从a到b的线段，但一端是闭合的（即该端点在线上），另一端是开放的（即该端点不在线上）。

实例解析：

区间[0, 1)包含所有从0（包括0）到1（不包括1）的实数。

区间(0, 1]包含所有从0（不包括0）到1（包括1）的实数。

实际应用：半开半闭区间在处理实际问题时尤为方便，尤其是当区间的边界条件不便于同时包含或排除时。例如，在排队论中，如果考虑从某一时刻开始（包含该时刻）到另一时刻结束（不包含该时刻）内的顾客到达情况，就可以使用半开半闭区间来描述这段时间范围。在计算机科学中，处理数组或列表的索引时，也经常用到半开半闭区间，如Python中的切片操作就是基于这种区间表示的。

综合应用与注意事项

在实际应用中，选择合适的区间表示方法对于确保准确性和避免歧义至关重要。以下几点值得注意：

1. 明确区间端点：在使用区间表示数值范围时，首先要明确哪些端点是包含的，哪些是不包含的。这直接影响了区间所覆盖的元素集合。

2. 选择最合适的表示方法：根据具体问题的性质，选择最合适的区间表示方法。例如，当描述一个物体的运动范围时，如果起点和终点都是明确的运动位置，可能更倾向于使用闭区间；而如果描述的是连续变化的过程，并且不希望包括某些特定的时刻或数值，开区间或半开半闭区间可能更为合适。

3. 避免混用区间表示方法：在同一数学表达式或描述中，应避免混用不同类型的区间表示方法，以免引起混淆。例如，