如何计算扇形的面积
扇形,作为圆的一部分,其面积的计算在几何学中占有重要地位。无论是在日常生活、工程设计还是科学研究中,了解并掌握扇形面积的计算方法都显得尤为重要。本文旨在全面介绍扇形面积的计算方法,帮助读者深入理解这一概念。
首先,我们需要明确扇形的基本概念。扇形是由圆心和圆上两点之间的弧以及连接这两点的半径所围成的图形。换句话说,扇形是圆的一个部分,其边界由一条弧和两条半径组成。扇形的面积与整个圆的面积有关,同时也受到扇形所占圆心角大小的影响。
在扇形面积的计算中,我们首先需要知道圆的半径(r)和扇形所占的圆心角(θ)。圆心角通常以度(°)或弧度(rad)为单位。为了简化计算,我们通常会将圆心角转换为弧度制,因为弧度制在计算中更为方便。圆心角与弧度的转换公式为:弧度 = 度数 × (π/180)。
接下来,我们介绍扇形面积的计算公式。扇形面积(A)的计算公式为:A = (1/2) × r^2 × θ,其中r为圆的半径,θ为扇形所占圆心角的弧度值。这个公式是扇形面积计算的基础,它表明扇形面积与半径的平方和圆心角的弧度值成正比。
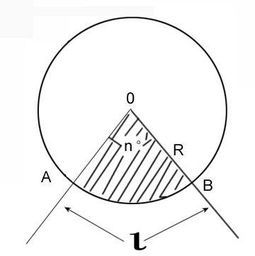
为了更直观地理解这个公式,我们可以将其与整个圆的面积进行比较。整个圆的面积公式为:A = π × r^2。由于一个完整的圆可以看作是一个圆心角为2π(或360°)的扇形,因此我们可以将扇形面积公式看作是整个圆面积公式的一个特例。当θ=2π时,扇形面积公式就变成了整个圆的面积公式。
现在,我们通过一个具体的例子来演示扇形面积的计算过程。假设我们有一个半径为5厘米的圆,其中一个扇形的圆心角为90°(或π/2弧度)。要计算这个扇形的面积,我们首先将圆心角转换为弧度制:θ = 90° × (π/180) = π/2。然后,我们将半径和圆心角的弧度值代入扇形面积公式中:A = (1/2) × 5^2 × (π/2) = (25/4)π 平方厘米。
除了上述的基本扇形面积计算公式外,还有一些特殊情况下的扇形面积计算方法。例如,当扇形是由一个给定的弦长和对应的圆心角确定时,我们可以通过弦长和圆心角来计算扇形的半径,进而求得扇形的面积。这种方法的关键在于利用弦长、半径和圆心角之间的几何关系来求解半径。
另外,当扇形是由一个给定的弧长和对应的半径确定时,我们可以直接利用弧长和半径来计算扇形的面积。这种方法利用了扇形面积与弧长和半径之间的直接关系。扇形面积的另一种表达式为:A = (1/2) × l × r,其中l为扇形的弧长。弧长与圆心角和半径的关系为:l = θ × r,其中θ为圆心角的弧度值。因此,我们可以将弧长公式代入扇形面积公式中,得到另一种计算扇形面积的方法:A = (1/2) × θ × r^2。这种方法在已知弧长和半径时更为方便。
在实际应用中,扇形面积的计算往往涉及到更复杂的几何图形和实际问题。例如,在计算扇形面积时可能需要考虑扇形的边界条件、与其他几何图形的相交关系以及实际问题的约束条件等。因此,在解决实际问题时,我们需要灵活运用扇形面积的计算方法,并结合实际情况进行具体分析。
此外,扇形面积的计算在几何学、物理学、工程学等领域中都有广泛的应用。在几何学中,扇形面积的计算是理解圆和扇形性质的基础;在物理学中,扇形面积的计算常用于描述和分析旋转物体的运动状态;在工程学中,扇形面积的计算则涉及到各种旋转机械和结构的设计和分析等方面。
总之,扇形面积的计算是几何学中的一个重要概念,它涉及到圆的性质、圆心角的度量以及几何图形的面积计算等方面。通过本文的介绍,读者可以全面了解扇形面积的计算方法,并能够在实际应用中灵活运用这些知识。无论是对于初学者还是对于需要深入理解扇形面积计算的读者来说,本文都提供了有价值的参考和指导。希望读者能够通过本文的学习,更好地掌握扇形面积的计算方法,并在实际生活中加以应用。
- 上一篇: 对联的正确贴法
- 下一篇: 如何挑选合适的玉镯子?
游戏攻略帮助你
更多+-
04/22
-
04/22
-
04/22
-
04/22
-
04/22









