二次函数的图像和性质有哪些？

在数学领域中，二次函数是一个极为重要的概念，它不仅是初等数学与高等数学之间的桥梁，更在实际问题中拥有广泛的应用。当我们谈及“二次函数的图像和性质”时，一系列丰富而生动的数学图景便跃然纸上。这些性质不仅揭示了二次函数本身的内在规律，还为我们解决实际问题提供了强有力的数学工具。

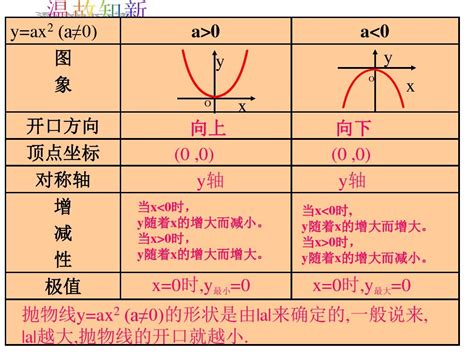
首先，我们需要明确什么是二次函数。一般地，形如y=ax^2+bx+c（其中a、b、c是常数，a≠0）的函数被称为二次函数。这个函数表达式中，x是自变量，y是因变量。二次函数的图像是一个抛物线，这个抛物线的开口方向、顶点位置以及对称轴等特征，都由函数表达式中的系数a、b、c决定。

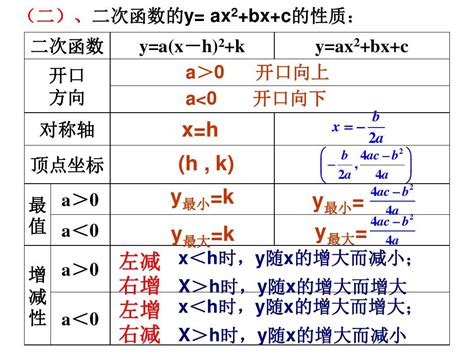
二次函数的图像——抛物线，具有鲜明的几何特征。当a>0时，抛物线开口向上，表示函数值随着x的增大而先减后增，具有最小值；当a<0时，抛物线开口向下，表示函数值随着x的增大而先增后减，具有最大值。这一性质在实际问题中尤为重要，它告诉我们，当面对一个具有二次函数关系的实际问题时，我们可以通过求解二次函数的极值来找到问题的最优解。

抛物线的顶点坐标是二次函数性质中的一个关键点。对于一般形式的二次函数y=ax^2+bx+c，其顶点坐标为(-b/2a, c-b^2/4a)。这个坐标不仅决定了抛物线的位置，还反映了二次函数的极值点。在实际应用中，我们常常需要找到这个极值点，以确定问题的最优解或最劣解。例如，在经济学中，成本函数、收益函数等往往呈现为二次函数形式，通过求解其极值点，我们可以找到成本最低或收益最大的生产规模。

抛物线的对称轴也是二次函数的一个重要性质。对于一般形式的二次函数y=ax^2+bx+c，其对称轴为直线x=-b/2a。这个性质告诉我们，抛物线在对称轴两侧是对称的，即对于任意一点P(x,y)在抛物线上，都有点P'(-b/2a-x, y)也在抛物线上。这一性质在解决某些对称性问题时尤为有用，它可以帮助我们简化计算过程，提高解题效率。

除了上述性质外，二次函数还具有与x轴的交点性质。当二次函数与x轴相交时，即y=0时，我们得到方程ax^2+bx+c=0。这个方程的解就是抛物线与x轴的交点横坐标。根据判别式Δ=b^2-4ac的值，我们可以判断方程的解的个数：当Δ>0时，方程有两个不相等的实数解，即抛物线与x轴有两个交点；当Δ=0时，方程有两个相等的实数解，即抛物线与x轴有一个交点（也即顶点在x轴上）；当Δ<0时，方程无实数解，即抛物线与x轴无交点。这一性质在解决实际问题时具有重要意义，它可以帮助我们判断问题的可行性或解的存在性。

在实际应用中，二次函数的图像和性质具有广泛的应用价值。例如，在物理学中，物体的自由落体运动、抛体运动等往往可以表示为二次函数关系；在经济学中，成本函数、收益函数等也常呈现为二次函数形式；在工程学中，桥梁、拱门等结构的形状设计也常利用二次函数的性质进行优化。此外，在信息技术领域，二次函数也被广泛应用于数据加密、图像处理等领域。

二次函数的图像和性质还为我们提供了一些重要的数学方法。例如，配方法是一种将一般形式的二次函数转化为顶点式的数学方法。通过配方法，我们可以轻松地找到二次函数的顶点坐标和对称轴方程。此外，求根公式也是一种重要的数学工具，它可以帮助我们求解二次方程并找到抛物线与x轴的交点坐标。这些数学方法不仅在数学学习中具有重要地位，还在实际问题解决中发挥着重要作用。

值得注意的是，虽然二次函数的图像和性质为我们提供了丰富的数学工具和方法，但在实际应用中我们还需要注意一些限制条件。例如，在某些实际问题中，我们可能需要对二次函数的定义域进行限制以确保问题的可行性；在某些情况下，我们还需要考虑二次函数的实际背景以选择适当的数学模型进行求解。

综上所述，“二次函数的图像和性质”是数学领域中一个极为重要的概念。它不仅揭示了二次函数本身的内在规律还为我们解决实际问题提供了强有力的数学工具。通过深入学习和理解二次函数的图像和性质我们可以更好地掌握这一数学工具并灵活地将其应用于实际问题解决中。无论是在学术研究还是在实际应用中二次函数的图像和性质都发挥着不可替代的作用并将继续为我们探索数学世界的奥秘提供有力的支持。