揭秘扇形面积的奥秘

在数学中，计算扇形的面积是一个常见且重要的任务。扇形是圆的一部分，由两个半径和一段圆弧围成。当我们需要求解扇形的面积时，通常会用到一些关键的数学公式和概念，如圆心角、半径和圆周率π。以下是一篇详细探讨扇形面积计算的文章，其中包含了多个关键词，以提高文章的曝光率。

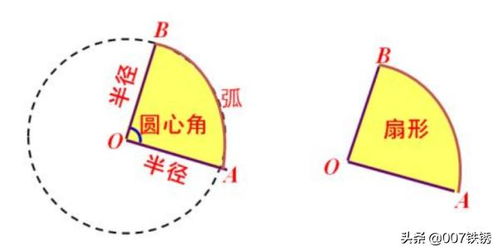
扇形面积的计算基于圆的面积，而圆的面积公式是π乘以半径的平方。扇形作为圆的一部分，其面积与圆心角有关。圆心角是扇形弧所对应的圆心角，通常以度数或弧度表示。为了计算扇形的面积，我们需要知道扇形的圆心角和半径。

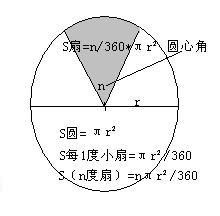
首先，让我们回顾一下圆的面积公式。圆的面积A等于π乘以半径r的平方，即A = πr²。这是计算扇形面积的基础。扇形面积的计算公式是扇形圆心角占整个圆的比例，再乘以圆的面积。如果用θ表示扇形的圆心角（以弧度为单位），那么扇形的面积A_扇形可以表示为：A_扇形 = (θ/2π) × πr²。简化后得到A_扇形 = (θ/2) × r²。

在实际应用中，圆心角通常以度数表示，因此我们需要将度数转换为弧度来计算扇形面积。弧度和度数之间的转换公式是：弧度 = 度数 × (π/180)。例如，如果扇形的圆心角是90度，那么对应的弧度是90 × (π/180) = π/2。

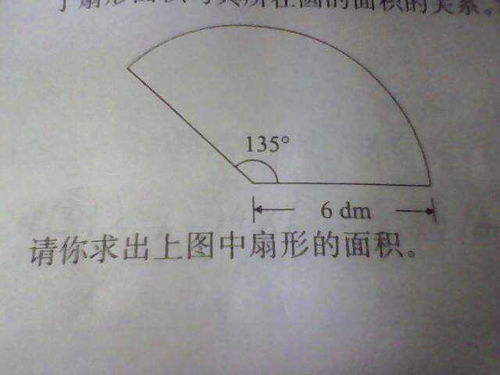
现在，让我们通过一个具体的例子来计算扇形的面积。假设我们有一个半径为5厘米的圆，其中一个扇形的圆心角是60度。首先，我们需要将60度的圆心角转换为弧度：60 × (π/180) = π/3。然后，我们将转换后的弧度和半径代入扇形面积的计算公式中：(π/3) ÷ 2 × 5² = (π/3) × 25 ÷ 2 = (25π/6) 平方厘米。

在计算扇形面积时，我们还需要注意一些常见的错误和陷阱。首先，确保使用正确的圆心角和半径值。如果圆心角以度数表示，一定要先转换为弧度再进行计算。其次，扇形面积的计算结果通常以平方厘米、平方米等面积单位表示，确保在计算过程中单位的一致性。

除了直接计算扇形面积外，我们还可以通过其他方法间接求解。例如，如果我们知道扇形的弧长和半径，可以使用弧长和半径的关系来计算扇形的圆心角，进而求解面积。扇形的弧长L等于圆心角θ（以弧度为单位）乘以半径r，即L = θ × r。通过这个公式，我们可以求出圆心角θ = L/r，然后将θ代入扇形面积的计算公式中。

此外，扇形面积的计算在几何学和实际应用中具有广泛的应用。在建筑设计、机械制造、地图制作等领域，经常需要计算扇形的面积。例如，在建筑设计中，扇形窗户或扇形屋顶的面积计算对于材料的选择和成本的估算至关重要。在机械制造中，扇形齿轮或扇形零件的面积计算有助于确定加工参数和工艺路线。在地图制作中，扇形区域的面积计算对于地图的比例尺和准确性具有重要意义。

为了提高扇形面积计算的准确性和效率，我们可以使用一些数学工具和软件。例如，计算器可以用于执行复杂的数学运算和单位转换。数学软件如Mathematica、MATLAB等可以用于进行精确的数值计算和图形绘制。这些工具可以大大简化扇形面积的计算过程，并帮助我们快速获得准确的结果。

总之，扇形面积的计算是数学中的一个重要问题，它涉及到圆的面积、圆心角、弧度等关键概念。通过掌握扇形面积的计算公式和常见的错误陷阱，我们可以更准确地计算扇形的面积，并在实际应用中发挥其重要作用。无论是在建筑设计、机械制造还是地图制作等领域，扇形面积的计算都扮演着不可或缺的角色。因此，我们应该注重扇形面积计算的学习和实践，不断提高自己的数学能力和应用能力。

在计算扇形面积时，我们还可以进一步探索其与其他几何形状的关系。例如，扇形可以看作是一个三角形在圆上的延伸，因此我们可以利用三角形的面积公式来辅助理解扇形面积的计算。同时，扇形也是圆的一部分，我们可以通过分割和组合不同的扇形来构建更复杂的几何形状，并计算它们的面积。

此外，扇形面积的计算还可以与其他数学知识相结合，如三角函数、微积分等。三角函数可以帮助我们计算扇形的边长和角度，微积分则可以帮助我们求解更复杂的扇形面积问题，如变半径扇形或不规则扇形的面积。

综上所述，扇形面积的计算是一个涉及多个数学概念和方法的复杂问题。通过掌握基本的扇形面积计算公式和常见的错误陷阱，结合数学工具和软件的应用，我们可以更准确地计算扇形的面积，并在实际应用中发挥其重要作用。同时，我们还可以通过探索扇形与其他几何形状的关系以及与其他数学知识的结合，进一步拓展扇形面积计算的应用领域和深度。