想知道二次函数对称轴在哪？教你一招轻松找到！

在数学中，二次函数是一个非常重要的概念，它广泛应用于各种领域，如物理学、工程学和经济学等。对于二次函数的学习和理解，一个关键的概念是其对称轴。对称轴不仅能帮助我们更直观地理解二次函数的性质，还能简化许多计算。那么，二次函数的对称轴怎么找呢？以下是详细的探讨。

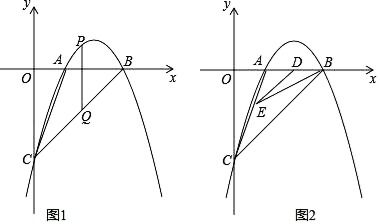
首先，我们需要明确什么是二次函数。一般地，形如y=ax²+bx+c（a≠0，a、b、c为常数）的函数，叫做二次函数。其中，a称为二次项系数，b为一次项系数，c为常数项。x是自变量，y是因变量。二次函数的图像是一条抛物线。这条抛物线可能开口向上或开口向下，具体取决于二次项系数a的正负。当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

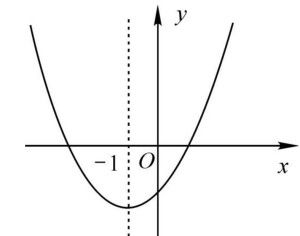
接下来，我们来看如何找到二次函数的对称轴。二次函数的对称轴是一条垂直于x轴的直线，其方程可以通过二次函数的系数来确定。具体来说，二次函数y=ax²+bx+c的对称轴方程为x=-b/(2a)。这个公式非常重要，它为我们提供了一种快速找到二次函数对称轴的方法。

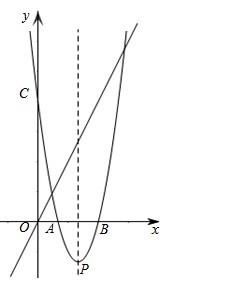
为了更好地理解这个公式，我们可以通过一些具体的例子来进行说明。

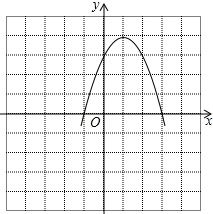
假设我们有一个二次函数y=2x²+4x+1。在这个函数中，a=2，b=4。根据对称轴的公式，我们可以计算出对称轴的方程为x=-4/(2×2)=-1。因此，这个二次函数的对称轴是直线x=-1。

现在，我们来看看这个对称轴在二次函数图像上的意义。由于二次函数的图像是一条抛物线，而对称轴是这条抛物线的对称中心线，所以抛物线关于对称轴对称。这意味着，如果我们在对称轴上找到一点，然后沿对称轴对折，我们会发现这一点与抛物线上的某一点重合。这个性质在解决某些问题时非常有用，比如求抛物线的最值问题。

在求抛物线的最值时，我们通常会先找到对称轴，然后确定对称轴与抛物线的交点。由于抛物线关于对称轴对称，所以交点就是抛物线的顶点。在开口向上的抛物线中，顶点是抛物线的最低点，也就是函数的最小值点；在开口向下的抛物线中，顶点是抛物线的最高点，也就是函数的最大值点。因此，通过找到对称轴和顶点，我们可以很容易地求出二次函数的最值。

除了求最值外，对称轴还在其他许多方面发挥着重要作用。比如，在解决二次不等式问题时，我们通常会先找到二次函数的对称轴和顶点，然后根据抛物线的开口方向和顶点位置来确定不等式的解集。此外，在解决与二次函数相关的几何问题时，对称轴也经常作为一个重要的参考线来使用。

那么，我们如何验证找到的对称轴是否正确呢？一种简单的方法是，我们可以在抛物线上选择两个对称的点，然后验证这两点关于对称轴对称。具体来说，我们可以先在对称轴上选择一个点作为基准点，然后在抛物线上分别找到这个基准点上方和下方的两个点。如果这两个点关于对称轴对称，那么我们就可以确认找到的对称轴是正确的。

另外，我们还可以通过绘图来验证对称轴的正确性。我们可以使用数学软件或绘图工具来绘制二次函数的图像，并在图像上标出对称轴。然后，我们可以观察抛物线是否关于对称轴对称。如果对称轴两侧的抛物线部分完全重合或镜像对称，那么我们就可以确认找到的对称轴是正确的。

值得注意的是，虽然对称轴是二次函数的一个重要性质，但在某些情况下，我们可能无法直接通过公式找到对称轴。比如，当二次函数的系数是未知数时，我们就需要通过解方程或其他方法来确定对称轴的方程。此外，在某些特殊情况下，如二次函数图像与x轴平行或重合时，对称轴的概念就不再适用。

总的来说，二次函数的对称轴是一个非常重要的概念，它不仅能帮助我们更直观地理解二次函数的性质，还能简化许多计算。通过掌握对称轴的公式和性质，我们可以更好地解决与二次函数相关的问题。同时，我们还需要注意特殊情况的处理方法，以确保我们的解题过程准确无误。

在学习二次函数的过程中，我们还需要注意一些常见的误区和易错点。比如，有些学生在计算对称轴时容易忽略系数的正负号或计算错误；有些学生在理解对称轴性质时容易混淆开口向上和开口向下的抛物线；还有些学生在解决实际问题时容易忽视对称轴的作用或误用对称轴的性质。因此，在学习和解题过程中，我们需要保持谨慎和细致的态度，认真理解和应用对称轴的相关知识。

通过以上探讨，我们可以得出结论：二次函数的对称轴是一条垂直于x轴的直线，其方程为x=-b/(2a)。通过掌握这个公式和对称轴的性质，我们可以更好地理解和应用二次函数的相关知识。同时，我们还需要注意特殊情况的处理方法和常见误区及易错点的避免方法，以确保我们的解题过程准确无误。希望这篇文章能帮助你更好地理解和掌握二次函数的对称轴相关知识。