揭秘二次函数:焦点与准线公式的奥秘
在数学的世界里,二次函数如同一座桥梁,连接着代数与几何的奇妙领域。当我们谈论二次函数的焦点和准线时,就像是探索一个隐藏在抛物线上的秘密花园。这些几何特性不仅丰富了我们对二次函数的理解,还在实际生活中有着广泛的应用,比如物理学中的抛物线运动、工程设计中的形状优化等。今天,就让我们一起揭开二次函数焦点和准线的神秘面纱,用通俗易懂的语言,深入了解它们的一般公式及其背后的意义。

二次函数的基本概念
首先,我们需要回顾一下二次函数的基础知识。二次函数,通常表示为y=ax²+bx+c(其中a≠0),是一个关于x的二次多项式函数。它的图像是一条抛物线,根据a的正负,抛物线开口向上(a>0)或向下(a<0)。

从几何视角看二次函数
在数学课上,我们可能更习惯于用代数方法解决二次函数问题,但几何视角能为我们提供不一样的洞见。想象一下,当你将一个物体沿着一定的角度抛出,它的轨迹就是一条抛物线。这条抛物线的形状、方向和位置,就取决于抛出的速度、角度和初始高度,而这些因素在数学上,正对应于二次函数的系数a、b和c。
焦点与准线的定义
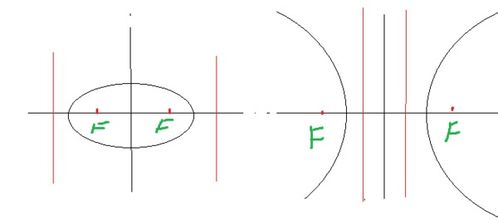
现在,让我们聚焦于抛物线上的两个特殊点——焦点和准线。焦点是抛物线上一个特殊的点,它具有这样的性质:抛物线上的任意一点到焦点的距离等于它到准线的距离。准线则是一条与抛物线平行(对于开口向左或向右的抛物线)或垂直(对于开口向上或向下的抛物线)的直线,它位于抛物线的对称轴的另一侧。
开口方向的影响
在探讨具体公式之前,需要注意的是,抛物线的开口方向会影响焦点和准线的位置。对于开口向上或向下的抛物线,焦点位于抛物线的对称轴上,而准线则是一条水平的直线。对于开口向左或向右的抛物线,情况则相反,焦点在抛物线的对称轴上,准线是一条垂直的直线。
焦点的一般公式
让我们先从焦点开始。对于一般形式的二次函数y=ax²+bx+c,我们可以通过以下步骤找到焦点的坐标:
1. 确定抛物线的对称轴:对称轴的方程是x=-b/(2a)。这是抛物线的顶点所在的直线,也是焦点所在的垂直线(对于开口向上或向下的抛物线)或水平线(对于开口向左或向右的抛物线,但这种情况下我们更关心y坐标的求解过程,因为x坐标就是对称轴的x值)。
2. 计算顶点的坐标:顶点的x坐标已经由对称轴给出,y坐标则是将x=-b/(2a)代入原函数求得,即y=a((-b/(2a))²)+b((-b/(2a)))+c。
3. 根据开口方向计算焦点的坐标:
对于开口向上或向下的抛物线,焦点的x坐标与顶点相同,y坐标则根据开口方向在顶点y坐标的基础上加上或减去|a|/4a(因为a的符号决定了开口方向,所以|a|/4a实际上给出了正确的距离且考虑了方向)。
对于开口向左或向右的抛物线,焦点的y坐标与顶点相同(如果顶点y坐标已知),x坐标则通过类似的逻辑计算得出,但这种情况下我们更常用的是通过顶点式和对称轴直接得出焦点x坐标。
然而,为了简化,通常我们使用顶点式y=a(x-h)²+k(其中(h,k)为顶点坐标)来直接计算焦点。对于开口向上或向下,焦点坐标为(h, k+|a|/4a);对于开口向左或向右,则根据具体情况调整。
准线的一般公式
接下来,我们来看准线的一般公式。准线的位置取决于抛物线的开口方向和顶点的位置:
对于开口向上或向下的抛物线,准线的方程是y=k-|a|/4a(其中(h,k)为顶点坐标)。这里,准线位于顶点y坐标的下方(开口向上)或上方(开口向下),距离等于|a|/4a。
对于开口向左或向右的抛物线,准线的方程是x=h±|a|/4a(正负号取决于抛物线的开口方向)。这里需要注意的是,虽然公式形式上看似与开口方向无关,但实际上是通过调整抛物线的标准方程来确保准线位置正确。在实际应用中,我们更常用的是根据顶点式和对称轴直接得出准线的x坐标(对于开口向左,是h-|a|/4a;对于开口向右,是h+|a|/4a)。
实际应用与直观理解
了解了焦点和准线的一般公式后,我们来看看它们在实际中的应用。在物理学中,抛体运动的轨迹就是一条抛物线,其焦点和
- 上一篇: 支付宝好友添加秘籍:轻松拓展你的社交圈
- 下一篇: 玩转指尖艺术:全面转笔教程大揭秘
新锐游戏抢先玩
游戏攻略帮助你
更多+-
12/26
-
12/26
-
12/26
-
12/26
-
12/26













