如何将角度转换为弧度公式是什么？

在数学和物理等领域，角度和弧度是两种常见的测量角的方式。虽然它们看似不同，但实际上有着密切的联系，可以通过简单的公式进行转换。理解角度与弧度的转换公式，不仅能帮助我们更好地进行数学计算，还能让我们更深入地理解三角函数、圆周运动等概念。

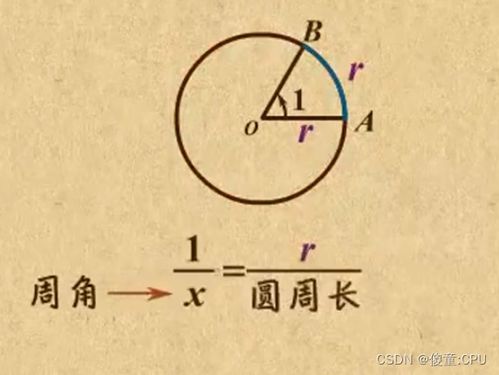
角度：我们熟悉的测量方式

提到角度，大家可能第一时间想到的是量角器上的刻度。角度是我们日常生活中非常熟悉的角的度量方式，通常以度（°）为单位。一个完整的圆周角是360度，而一个直角则是90度。角度的概念相对直观，适用于很多日常生活中的场景，比如测量转角、判断方向等。

弧度：更自然的测量方式

与角度不同，弧度是另一种测量角的方式，它在数学和物理学中更为常用。弧度制的基本思想是将圆周的弧长与半径相关联。一个完整的圆周角对应的弧度是2π，而一个直角对应的弧度是π/2。弧度的引入，使得很多数学公式（尤其是涉及三角函数和圆周运动的公式）变得更加简洁和优美。

为什么要进行角度与弧度的转换？

在许多科学计算和理论推导中，使用弧度制比角度制更方便。弧度制与圆的性质、三角函数等数学概念有着天然的联系，因此在涉及这些概念的公式和定理中，弧度制往往能让公式更加简洁和易于推导。例如，三角函数的导数公式在弧度制下更加直观和简单。此外，在物理学中，特别是涉及到圆周运动、振动和波动等现象时，弧度制也更为常用。

角度与弧度转换公式

现在，我们来详细介绍角度与弧度之间的转换公式。

角度转弧度

要将角度转换为弧度，我们可以使用以下公式：

弧度 = 角度 × (π/180)

这个公式的原理很简单：一个完整的圆周角是360度，对应的弧度是2π。因此，将角度乘以π/180，就可以得到对应的弧度值。

例如，要将90度转换为弧度，我们可以这样计算：

弧度 = 90 × (π/180) = π/2

弧度转角度

同样地，要将弧度转换为角度，我们可以使用以下公式：

角度 = 弧度 × (180/π)

这个公式的原理是：一个完整的圆周角对应的弧度是2π，而角度是360度。因此，将弧度乘以180/π，就可以得到对应的角度值。

例如，要将π/3弧度转换为角度，我们可以这样计算：

角度 = (π/3) × (180/π) = 60°

应用实例

为了更好地理解角度与弧度的转换，我们可以看一些实际应用中的例子。

三角函数中的应用

三角函数（如正弦、余弦、正切等）是数学中的一类重要函数，它们在角度制和弧度制下都有定义。但是，在弧度制下，三角函数的很多性质（如周期性、导数等）都表现得更加简洁和直观。因此，在进行三角函数的相关计算时，通常会将角度转换为弧度。

例如，要求sin(30°)，我们可以先将30°转换为弧度，即30° × (π/180) = π/6，然后计算sin(π/6) = 1/2。

圆周运动中的应用

在物理学中，圆周运动是一个常见的现象。在描述圆周运动的角速度、角加速度等物理量时，通常使用弧度制。这是因为弧度制与圆的性质（如半径、弧长等）有着紧密的联系，使得相关公式的推导和计算更加方便。

例如，一个质点以恒定的角速度ω绕圆心做圆周运动。如果ω的单位是弧度/秒，那么质点在t秒内转过的角度（以弧度计）就是ωt。如果我们用角度制来表示角速度（如度/秒），那么在计算质点转过的角度时就需要进行额外的转换。

注意事项

在进行角度与弧度的转换时，需要注意以下几点：

1. 单位一致性：在进行涉及角度和弧度的计算时，要确保所有的角度值都使用相同的单位（要么都是角度制，要么都是弧度制），否则会导致计算错误。

2. 计算精度：在进行角度与弧度的转换时，由于π是一个无理数，因此转换结果可能是一个近似值。在实际应用中，需要根据计算精度要求选择合适的近似值。

3. 符号问题：在角度制中，角度可以是正数也可以是负数，表示顺时针或逆时针旋转的方向。在弧度制中同样如此。在进行转换时，要注意保持角度的符号不变。

如何记忆这些公式？

角度与弧度的转换公式虽然简单