如何计算弧度
弧度应该怎么算
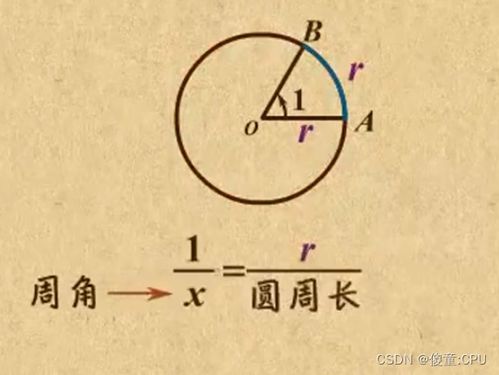
在数学和物理学中,弧度是一种角度的测量单位,它基于圆的半径长。与度数不同,弧度提供了一种更自然的方式来描述圆上的弧长与半径之间的关系。理解弧度概念以及如何进行计算,对于深入学习三角函数、微积分等领域至关重要。下面,我们将详细介绍弧度的定义、计算方法以及在实际问题中的应用。
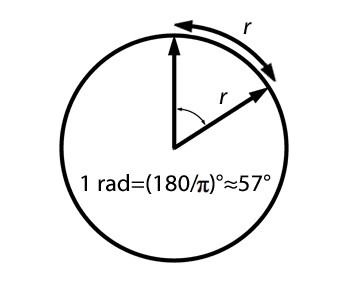
一、弧度的定义
弧度是通过将圆上的一段弧长与圆的半径进行比较来定义的。具体来说,如果一个圆的弧长等于该圆的半径,则这段弧所对应的圆心角被定义为1弧度。换句话说,弧度是衡量圆心角大小的另一种方式,它直接反映了弧长与半径之间的比例关系。
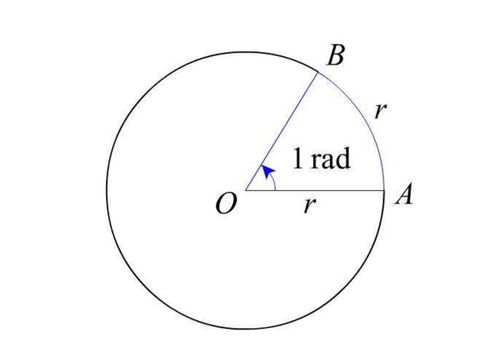
二、弧度的计算方法
1. 基础公式
弧度的计算公式是弧长除以半径,即:
弧度 = 弧长 / 半径
这个公式是弧度定义的直接应用,它告诉我们如何根据弧长和半径来计算圆心角的弧度值。
2. 单位圆上的弧度计算
在单位圆(半径为1的圆)上,弧长就等于弧度。因此,我们可以直接通过测量单位圆上某段弧的长度来得到对应的弧度值。例如,单位圆上四分之一圆的弧长为π/2(圆的周长为2π,四分之一圆即为π/2),所以对应的圆心角为π/2弧度。
3. 常见角度的弧度表示
为了将常见的角度转换为弧度,我们需要知道角度与弧度之间的转换关系。具体来说,180度等于π弧度,90度等于π/2弧度,45度等于π/4弧度,以此类推。这个转换关系是基于圆的周长和直径的比值π(约等于3.14159)得出的。
三、弧度与度数的转换
1. 度数转弧度
要将度数转换为弧度,我们可以使用以下公式:
弧度 = 度数 × π / 180
这个公式是根据弧度与度数之间的比例关系得出的。通过乘以π/180,我们可以将度数转换为弧度。
2. 弧度转度数
要将弧度转换为度数,我们可以使用以下公式:
度数 = 弧度 × 180 / π
这个公式是度数转弧度公式的逆运算。通过乘以180/π,我们可以将弧度转换为度数。
四、弧度在三角函数中的应用
三角函数(如正弦、余弦、正切等)是数学中的重要工具,它们在物理学、工程学等领域有着广泛的应用。在弧度制下,三角函数的定义更加直观和简洁。例如,正弦函数定义为对边与斜边之比,在弧度制下,这个比值恰好等于单位圆上对应角度的y坐标值。同样地,余弦函数定义为邻边与斜边之比,它等于单位圆上对应角度的x坐标值。这种定义方式使得三角函数在弧度制下具有更好的性质,如周期性、导数等。
五、弧度在微积分中的应用
在微积分中,弧度制也扮演着重要的角色。例如,在求圆的周长和面积时,我们使用的公式C=2πr和S=πr²都是基于弧度制得出的。此外,在求解与圆相关的导数、积分等问题时,弧度制也提供了更加简洁和直观的解法。例如,在求解圆的切线斜率时,我们可以直接利用弧度制下的导数公式(即正弦函数和余弦函数的导数)来求解。
六、弧度在实际问题中的应用
弧度制不仅在数学和物理学中有广泛的应用,而且在日常生活中也扮演着重要的角色。例如,在工程设计、机械设计等领域中,我们经常需要计算圆的弧长、角度等参数,这些计算都离不开弧度制。此外,在计算机科学中,弧度制也被广泛应用于图形处理、动画制作等领域。在这些领域中,我们需要对圆的形状进行精确的描述和控制,而弧度制为我们提供了一种更加自然和直观的方式来描述圆上的弧长和角度。
七、总结
弧度是一种重要的角度测量单位,它基于圆的半径长来定义圆心角的大小。通过理解弧度的定义和计算方法,我们可以更加深入地理解三角函数、微积分等数学概念,并在实际问题中灵活应用这些知识。在计算弧度时,我们可以使用弧长除以半径的公式,也可以利用单位圆上的弧长来直接得到对应的弧度值。此外,我们还需要注意弧度与度数之间的转换关系,以便在不同的应用场景中进行灵活切换。通过不断学习和实践,我们可以更好地掌握弧度制的计算方法和应用技巧,为未来的学习和工作打下坚实的基础。
- 上一篇: 蓝莓清洗全攻略:轻松洗净小妙招
- 下一篇: 家常黄鳝烹饪秘籍:营养美味双全
新锐游戏抢先玩
游戏攻略帮助你
更多+-
02/07
-
02/07
-
02/07
-
02/07
-
02/07









