揭秘平行四边形对角线长度的神奇计算公式
在几何学的奇妙世界里,平行四边形以其独特的性质和广泛的应用,成为了我们探索形状与空间奥秘的重要一环。而谈及平行四边形的核心特性之一,不得不提的就是其对角线的计算。想象一下,一个平行四边形,在二维平面上优雅地铺展,它的对角线如同桥梁,连接着对角顶点,不仅承载着结构的稳定性,更隐藏着数学之美。今天,就让我们一同揭开平行四边形对角线计算公式的神秘面纱,感受几何与代数交织的魅力。
平行四边形:几何舞台上的舞者
平行四边形,这个看似简单的四边形家族成员,却拥有着不凡的特质。它的两组对边平行且等长,这一基本定义就为其赋予了独特的对称性和平衡感。在平面几何中,平行四边形不仅是基础图形,更是构建复杂图形和解决实际问题的重要工具。从建筑设计到电子电路设计,从物理模型的构建到计算机图形学的应用,平行四边形的身影无处不在,而其对角线的计算,则是解锁这些应用的关键之一。
对角线:平行四边形中的隐形纽带
在平行四边形中,对角线扮演着至关重要的角色。它们不仅连接了对角顶点,形成了两条交叉的线段,更重要的是,这两条对角线之间存在着一系列令人着迷的关系和性质。比如,它们的长度可以通过特定的公式计算得出;它们互相平分,即交点为对角线的中点;在特殊情况下,如矩形或正方形中,对角线还相等且垂直于彼此。这些性质不仅丰富了平行四边形的内涵,也为解决相关问题提供了强有力的数学工具。
揭秘:平行四边形对角线计算公式
那么,如何计算平行四边形的对角线长度呢?这里,我们就要引入一个简单而强大的公式,它能够帮助我们快速准确地找到答案。
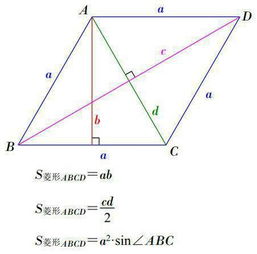
首先,设平行四边形的相邻两边分别为a和b,它们之间的夹角为θ(注意,这里的θ是两边向量之间的夹角,而非内角)。根据向量运算和余弦定理,我们可以推导出平行四边形的两条对角线长度公式:
第一条对角线(假设为d1)的长度公式为:d1 = √(a² + b² - 2ab·cosθ)
第二条对角线(假设为d2)的长度公式为:d2 = √(a² + b² + 2ab·cosθ)
这两个公式看似复杂,实则蕴含着深刻的几何意义。它们将平行四边形的边长、夹角与对角线长度紧密地联系在一起,展示了数学中的和谐与统一。通过这两个公式,我们只需知道平行四边形的任意两边长度及它们之间的夹角,就能轻松计算出对角线的长度,这无疑大大简化了计算过程,提高了效率。
实战演练:公式的应用
理论总是需要实践的检验。让我们通过一个具体的例子来演示如何运用上述公式计算平行四边形的对角线长度。
假设有一个平行四边形,其相邻两边长度分别为6厘米和8厘米,且这两边之间的夹角为60°(π/3弧度)。根据对角线计算公式,我们可以得到:
第一条对角线d1的长度为:d1 = √(6² + 8² - 2×6×8×cos(60°)) = √(36 + 64 - 96×0.5) = √(100 - 48) = √52 ≈ 7.21厘米
第二条对角线d2的长度为:d2 = √(6² + 8² + 2×6×8×cos(60°)) = √(36 + 64 + 96×0.5) = √(100 + 48) = √148 ≈ 12.17厘米
通过简单的代入和计算,我们就得出了平行四边形的两条对角线长度。这个过程不仅展示了公式的实用性,也让我们更加深刻地理解了平行四边形对角线之间的数学关系。
深入探索:公式的推导与理解
虽然上述公式已经足够我们进行对角线长度的计算,但知其然更要知其所以然。接下来,我们简要探讨一下这些公式的推导过程,以便更好地理解其背后的数学原理。
首先,我们可以将平行四边形的两边看作是两个向量,利用向量的数量积公式和余弦定理,我们可以推导出对角线长度的表达式。具体来说,如果我们把平行四边形的一条边看作是从原点出发的向量a,另一条边看作是从a的终点出发的向量b,那么对角线的向量和就可以表示为a+b。根据向量模长的计算公式和余弦定理,我们可以得到对角线长度的平方等于(a+b)²,即a² + 2a·b + b²。其中,a·b表示向量a和b的数量积,它等于|a|×|b|×cosθ,即两边长度之积与它们之间夹角的余弦的乘积。将这一结果代入上述公式,并注意到向量a和b的模长分别等于平行四边形的两边长度a和b,我们就可以得到对角线长度的平方的表达式,进而开方得到对角线的长度
- 上一篇: 家常蛋卷的美味制作秘籍
- 下一篇: 一般过去时的语法结构详解
新锐游戏抢先玩
游戏攻略帮助你
更多+-
02/08
-
02/08
-
02/08
-
02/08
-
02/08









