角度制和弧度制转换公式详解

在数学的浩瀚宇宙中，角度与弧度如同夜空中最亮的双子星，它们各自闪耀却又紧密相连。无论你是初学者还是资深数学爱好者，掌握角度制和弧度制的转化公式，都是通往更深层次数学探索的必经之路。今天，就让我们一同揭开这两大度量体系之间的神秘面纱，探索它们之间转换的奥秘，让你的数学之旅更加精彩纷呈！

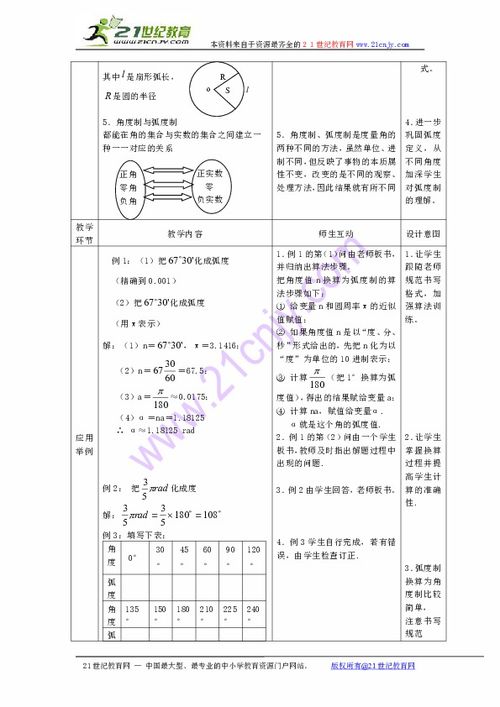
在数学的世界里，角度与弧度是描述旋转量的两种基本方式。角度制，这个我们从小耳熟能详的度量标准，用度（°）作为单位，直观易懂。而弧度制，则像是数学界的隐士，用弧度（rad）来衡量旋转的角度，它更加符合数学运算的简洁与美感。这两种度量方式虽然看似不同，实则通过一套神奇的转化公式紧密相连，共同构建出数学旋转的宏伟蓝图。

首先，让我们从基础出发，理解角度制与弧度制的本质区别。角度制，正如其名，是以度为单位来度量角的大小的。一个完整的圆周被等分为360度，而直角则恰好是其中的四分之一，即90度。这种度量方式直观易懂，非常适合日常生活中的简单计算。然而，在数学的深入探索中，我们往往会发现角度制在某些情况下显得繁琐且不够灵活。

此时，弧度制便应运而生。弧度制以弧长与半径的比值来定义角的大小，即一个角的弧度值等于其所夹弧长与所在圆的半径之比。这种定义方式使得弧度制在数学运算中更加简洁高效，特别是在微积分、三角函数等领域，弧度制更是不可或缺的工具。

那么，如何在这两种度量体系之间自由穿梭呢？这就需要我们掌握角度制与弧度制的转化公式。

角度制转弧度制的公式为：弧度 = 角度 × π / 180。这个公式告诉我们，要将一个角度值转换为弧度值，只需将其乘以π并除以180即可。例如，要将90度转换为弧度，只需计算90 × π / 180 = π / 2 弧度。这样，我们就能够轻松地在角度制与弧度制之间进行转换，为后续的数学运算打下基础。

反过来，弧度制转角度制的公式则为：角度 = 弧度 × 180 / π。同样地，这个公式帮助我们将弧度值转换为角度值。例如，要将π / 4弧度转换为角度，只需计算π / 4 × 180 / π = 45度。通过这两个公式，我们可以实现角度制与弧度制之间的无缝转换，让数学运算更加灵活便捷。

在掌握了这些基本公式后，我们还需要通过实例来加深理解。比如，在解决三角函数问题时，我们经常需要将角度值转换为弧度值来进行计算。因为三角函数在弧度制下具有更简洁的性质和公式，如正弦函数sin(x)在弧度制下的周期为2π，而在角度制下则为360度。这种差异使得在弧度制下求解三角函数问题更加直观和高效。

再比如，在微积分的学习中，我们经常会遇到与圆的弧长、扇形的面积等相关的计算。这些计算都需要用到弧度制来简化问题。例如，计算一个半径为r、圆心角为θ（弧度制）的扇形的面积时，我们可以直接使用公式S = 1/2 r²θ，而无需将角度值转换为弧度值再进行计算。这种简洁性正是弧度制在微积分中的独特魅力所在。

此外，掌握角度制与弧度制的转化公式还能够帮助我们更好地理解一些数学现象和定理。比如，欧拉公式e^(iθ) = cosθ + isinθ（其中e是自然对数的底数，i是虚数单位）在弧度制下才成立。这个公式将三角函数与复数紧密地联系在一起，揭示了数学世界中的深刻联系和奥秘。而如果我们试图在角度制下应用这个公式，就会发现它变得复杂且难以解释。

综上所述，角度制与弧度制是数学中不可或缺的两大度量体系。它们各自具有独特的优点和适用场景，而掌握它们之间的转化公式则是我们深入探索数学世界的钥匙。通过不断练习和应用这些公式，我们可以更加灵活地运用角度制和弧度制来解决实际问题，提高数学运算的效率和准确性。

当然，在学习和运用的过程中，我们也要注意避免一些常见的误区。比如，在计算三角函数值时，一定要确保输入的角度值已经转换为弧度值；在求解与圆的弧长、扇形的面积等相关的计算问题时，也要牢记使用弧度制来简化问题。只有这样，我们才能真正掌握角度制与弧度制之间的转换技巧，让数学成为我们探索世界的得力助手。

最后，让我们再次回顾一下角度制与弧度制的转化公式：弧度 = 角度 × π / 180；角度 = 弧度 × 180 / π。这两个公式不仅是我们解决数学问题的工具，更是我们理解数学世界奥秘的钥匙。让我们带着这份知识，继续在数学的海洋中遨游，探索更多