揭秘宇宙级大数：葛立恒数究竟有多惊人？

葛立恒数，这一数学领域的非凡成就，以其惊人的大小和独特的来源，引起了广泛的关注与讨论。这个数究竟有多大？为了解答这一问题，我们需要从其起源、定义、与常见大数的比较，以及它在数学和科学中的应用等多个方面进行深入探讨。

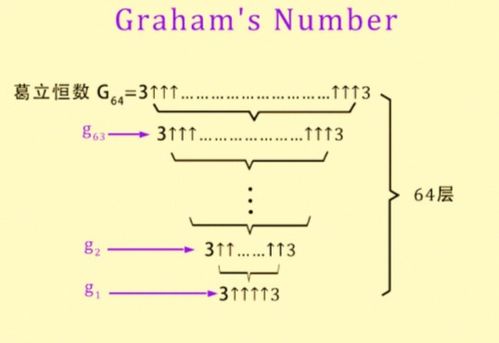
葛立恒数最初源自美国数学家葛立恒在研究拉姆齐理论时的一个问题。拉姆齐理论是组合数学的一个重要分支，它探讨了当一组对象足够大时，这些对象中总会存在某种特定的结构或性质。葛立恒在解决一个与拉姆齐理论相关的问题时，意外地构造出了一个极为庞大的数，这个数后来被命名为葛立恒数。

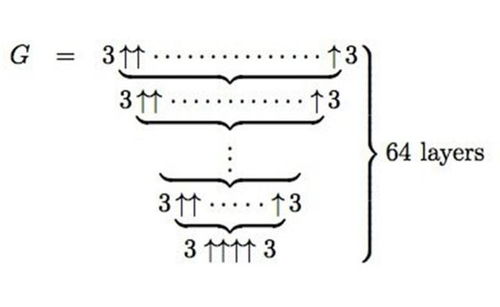
葛立恒数的具体定义相对复杂，但可以通过一个直观的例子来近似理解其大小。假设有一个足够大的二维平面，上面布满了红色和蓝色的点。葛立恒数就是这样一个数：当平面上的点的数量达到葛立恒数时，无论这些点如何分布，都可以找到一个由红色或蓝色点构成的边长为5的正方形（即四个顶点都是同色点的正方形）。这个定义中的“足够大”是相对的，因为葛立恒数远远超出了我们日常所能想象的数量级。

为了更直观地感受葛立恒数的大小，我们可以将其与一些常见的大数进行比较。例如，阿伏伽德罗常数（约为6.022×10^23）表示了1摩尔物质所含有的基本单位（如原子或分子）的数量。这个数字虽然庞大，但与葛立恒数相比，却显得微不足道。再比如，宇宙中的星星数量估计约为10^23到10^24个，这个数字同样无法与葛立恒数相提并论。实际上，葛立恒数的大小已经远远超出了我们能够用常规方式表达和理解的范畴。

那么，葛立恒数究竟是如何构造出来的呢？这涉及到一些高深的数学知识和技巧。简单来说，葛立恒数是通过递归和嵌套的方式构造出来的。在这个过程中，每一个递归步骤都会使得数的规模呈指数级增长。这种增长方式使得葛立恒数在极短的时间内就达到了一个令人难以置信的庞大数值。

葛立恒数的构造过程虽然复杂，但它在数学和科学领域的应用却是广泛的。首先，在组合数学中，葛立恒数为我们提供了一个衡量组合结构复杂性的重要标尺。通过比较不同组合结构所需的点的数量与葛立恒数的大小，我们可以直观地感受到这些结构的复杂性和差异性。

其次，在理论计算机科学中，葛立恒数也扮演着重要的角色。计算机科学中的许多问题都涉及到对大量数据的处理和分析。在处理这些问题时，我们需要设计高效的算法和数据结构来降低计算复杂度和存储空间。葛立恒数为我们提供了一个理论上的上限，即当数据量达到葛立恒数时，任何算法和数据结构都将面临巨大的挑战。这促使我们在设计算法和数据结构时更加注重效率和优化。

此外，葛立恒数还在物理学、天文学等领域中发挥着潜在的作用。例如，在宇宙学中，我们试图理解宇宙的起源、演化和结构。在这个过程中，我们需要处理大量的物理数据和观测结果。葛立恒数为我们提供了一个理论上的参考，即当宇宙中的粒子数量或事件数量达到葛立恒数时，我们可能需要重新审视现有的物理理论和数学模型。

当然，葛立恒数作为一个数学上的极端例子，其实际应用场景可能并不常见。但这并不意味着它没有价值或意义。相反，葛立恒数的存在和构造过程为我们提供了一种思考数学和科学问题的新视角和方法。它让我们意识到，在数学的海洋中，还有许多未知和神秘等待我们去探索和发现。

值得一提的是，尽管葛立恒数的大小令人惊叹，但它并不是数学中最大的数。在数学领域，存在着许多比葛立恒数还要庞大的数，如TREE(3)、SSCG(3)等。这些数同样是通过递归和嵌套的方式构造出来的，但它们的规模和复杂性远远超过了葛立恒数。这些数的存在进一步证明了数学世界的无限广阔和深邃。

总之，葛立恒数作为数学领域的一个非凡成就，以其惊人的大小和独特的来源引起了广泛的关注与讨论。通过对其起源、定义、与常见大数的比较以及在数学和科学中的应用等方面的探讨，我们可以更加深入地理解这个数的意义和价值。同时，葛立恒数的存在也为我们提供了一种思考数学和科学问题的新视角和方法，激励着我们不断探索和发现未知的数学世界。在未来的研究和探索中，我们期待能够发现更多类似葛立恒数的数学奇迹，为人类的智慧和文明贡献更多的力量。