揭秘：法拉第常数的确切数值是多少？

法拉第常数，一个在近代科学研究中占据重要地位的物理常数，它代表了每摩尔电子所携带的电荷，单位C/mol。这一常数的存在不仅为我们理解电化学反应提供了关键的桥梁，而且在电化学、生物学、分子动力学模拟等多个领域都发挥着重要的作用。

首先，我们需要明确法拉第常数的定义和来源。法拉第常数（F）是由英国物理学家迈克尔·法拉第在19世纪初通过一系列的电解实验得出的。法拉第发现，在电解过程中，析出的物质的质量与通过电解池的电量成正比，这一关系被称为法拉第电解定律。由此，法拉第提出了法拉第常数的概念，它代表了电流与电极之间的关系，也即是电荷与物质之间的关系。法拉第常数的重要性在于，它提供了一个将电荷与物质的量联系起来的桥梁，使得我们可以通过测量电流和反应速率来计算电量和物质的量。

法拉第常数的符号通常用F表示，其数值约为96485库仑每摩尔（C/mol）。这个数值表示每摩尔电荷通过一个电化学反应所需的电子数。具体而言，1F的电量可以在电化学反应中产生96485库仑的电流。这一数值是由美国国家标准局依据电解实验得到的，并被认为是最具有权威性的。法拉第常数的数值可以通过阿伏伽德罗常数NA（粒子数N与物质量n的比值）与元电荷e（电荷的基本电荷或大小）的积来计算得出，即F=NA×e。其中，阿伏伽德罗常数的值约为6.02214076×10^23mol^-1，元电荷的值约为1.60217663410×10^-19C。

在电化学领域，法拉第常数是一个至关重要的物理常数。它将电量与物质的量联系起来，为我们理解电化学反应提供了关键的桥梁。电化学反应中，电荷通过电解质溶液中的电解质进行传递，这种传递过程是通过电极上的氧化还原反应来实现的。法拉第常数可以帮助我们衡量电荷转移的速率，以及计算电荷的数量。根据法拉第方程，电流I与电量Q之间的关系可以表示为I=nFv，其中n是电荷的数量（以mol为单位），v是反应的速率。通过测量电流和反应速度，我们可以使用法拉第常数来计算电量。

在实际应用中，法拉第常数在电解质的浓度计算中也非常重要。根据法拉第定律，电流与电解质浓度之间存在线性关系。通过测量电流和浓度，我们可以使用法拉第常数来计算反应速率。在电解过程中，法拉第常数可以用于计算电解池中析出的物质的量。通过测量电解过程中析出的物质的量和通过电解池的电量，我们就可以计算出法拉第常数。此外，法拉第常数还可以用于计算电池的电量，即电池所能提供的总电荷量。在设计和优化新型电池时，法拉第常数也发挥着重要的作用，它可以帮助我们提高电池的能量密度和循环寿命。

除了在电化学领域中的应用，法拉第常数还在其他科学领域中得到了广泛的应用。例如，在生物学和生物化学中，法拉第常数用于测量电化学反应中涉及的生物分子的数量。在分子动力学模拟中，法拉第常数可用于计算电荷转移的速率。这些应用都体现了法拉第常数作为物理常数的重要性和实用性。

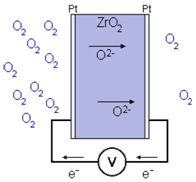
为了更好地理解法拉第常数，我们需要了解电化学反应的基本原理。在电化学反应中，电荷通过电解质溶液中的电解质进行传递，这种传递过程是通过电极上的氧化还原反应来实现的。氧化还原反应是电化学反应的核心，它涉及到电子的转移和化合价的变化。通过氧化还原反应，电荷得以在电解质溶液中传递，从而实现电能的转化和化学能的释放。法拉第常数在描述这种电荷传递过程中起着至关重要的作用。

此外，法拉第常数还与阿伏伽德罗常数和元电荷等物理常数密切相关。阿伏伽德罗常数代表了粒子数与物质量之间的比值，是描述物质微观结构的重要常数。元电荷则代表了电荷的基本单位，是描述电荷大小的基础。法拉第常数是这两个常数的乘积，它将物质的微观结构和电荷的基本单位联系起来，为我们理解电化学反应提供了更加深入的视角。

随着科技的不断发展，法拉第常数在未来的科学研究中将会发挥更加重要的作用。在电化学领域，法拉第常数将用于研究和开发更加高效的电化学催化剂和电化学传感器。这些新型材料和器件的出现将极大地推动电化学领域的发展和应用。同时，法拉第常数也将为其他科学领域的研究提供有力的支持和帮助。

总之，法拉第常数是近代科学研究中重要的物理常数之一。它代表了每摩尔电子所携带的电荷量，将电荷与物质的量联系起来。在电化学领域，法拉第常数是一个至关重要的物理常数，它为我们理解电化学反应提供了关键的桥梁。通过测量电流和反应速率，我们可以使用法拉第常数来计算电量和物质的量。此外，法拉第常数还在生物学、分子动力学模拟等领域中得到了广泛的应用。随着科技的不断发展，法拉第常数在未来的科学研究中将会发挥更加重要的作用。

对于科研人员和学生来说，深入了解法拉第常数的重要性和应用是非常重要的。通过学习和掌握法拉第常数的