卷积运算的定义及公式
卷积运算,这一看似复杂的数学概念,实则广泛运用于通信技术、图像处理、信号处理等多个领域,成为现代科技中不可或缺的一部分。本文将从多个维度深入剖析卷积运算公式,带您领略其背后的奥秘。
卷积运算的基本概念
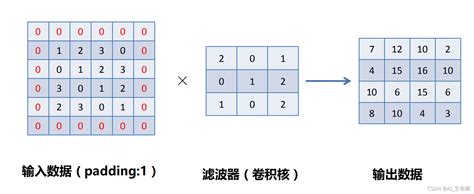
卷积运算,顾名思义,是一种通过“卷绕”和“积累”来完成的运算。具体来说,卷积运算是指从图像的左上角开始,开一个与模板同样大小的活动窗口,窗口图像与模板像元对应起来相乘再相加,并用计算结果代替窗口中心的像元亮度值。然后,活动窗口向右移动一列,并作同样的运算。以此类推,从左到右、从上到下,即可得到一幅新图像。这种运算方式不仅在图像处理中发挥着重要作用,还广泛应用于信号处理和滤波技术中。
数学维度的卷积运算公式
在数学上,卷积运算通常表示为两个函数f(x)和g(x)的乘积的积分,即:
(f∗g)(t)=∫f(τ)g(t−τ)dτ(f imes g)(t) = \int f(\tau)g(t-\tau) \, d\tau(f∗g)(t)=∫f(τ)g(t−τ)dτ
这个公式描述了如何通过两个函数的相互作用来生成一个新的函数。在这里,f(τ)和g(t-τ)是两个参与运算的函数,它们通过积分运算进行“卷绕”和“积累”,最终得到一个新的函数(f∗g)(t)。
为了更直观地理解这个公式,我们可以将其类比为信号处理中的滤波过程。假设f(x)是一个输入信号,g(x)是一个滤波器,那么(f∗g)(t)就是经过滤波器处理后的输出信号。在这个过程中,滤波器g(x)会遍历输入信号f(x)的每一个点,通过乘法运算和积分运算来提取信号的特征,从而得到一个新的信号。
图像处理维度的卷积运算
在图像处理中,卷积运算通常用于实现图像的滤波和边缘检测等功能。以空间域滤波为例,卷积运算通过将一个模板(或称为滤波器)应用于图像的每一个像素点,来提取图像的特征或进行去噪等处理。
具体来说,假设有一个M×N的模板h和一幅大小为P×Q的图像f,那么卷积运算的结果是一幅大小为(P-M+1)×(Q-N+1)的新图像g。新图像g中的每一个像素点都是通过将模板h与图像f中对应位置的像素点进行乘法运算和加法运算得到的。
这种运算方式不仅可以用于图像的平滑处理,还可以用于边缘检测、锐化等处理。例如,在边缘检测中,通常会使用一个特定的模板(如Sobel算子、Prewitt算子等)来提取图像的边缘特征。这些模板通过卷积运算与图像进行相互作用,从而提取出图像中的边缘信息。
信号处理维度的卷积运算
在信号处理领域,卷积运算同样发挥着重要作用。以线性时不变系统为例,系统的输出信号y(t)可以表示为输入信号x(t)与系统的冲击响应h(t)的卷积:
y(t)=(x∗h)(t)=∫x(τ)h(t−τ)dτy(t) = (x imes h)(t) = \int x(\tau)h(t-\tau) \, d\tauy(t)=(x∗h)(t)=∫x(τ)h(t−τ)dτ
这个公式描述了线性时不变系统如何通过输入信号和冲击响应的卷积运算来生成输出信号。在这个过程中,冲击响应h(t)描述了系统对输入信号的响应特性,而卷积运算则实现了输入信号与冲击响应的相互作用。
实际应用维度的卷积运算
卷积运算在实际应用中具有广泛的应用价值。在通信技术中,卷积运算可以用于实现信号的编码和解码;在图像处理中,卷积运算可以用于图像的滤波、边缘检测、特征提取等;在信号处理中,卷积运算可以用于信号的滤波、去噪、识别等。
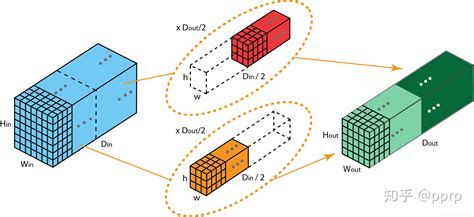
以深度学习中的卷积神经网络(CNN)为例,卷积运算被广泛应用于图像识别和分类等任务中。卷积神经网络通过构建多个卷积层来提取图像的特征信息,从而实现图像的高效识别和分类。在这个过程中,卷积运算通过卷积核(或称为滤波器)与图像的相互作用来提取图像的特征信息,并通过池化层、全连接层等结构来实现特征信息的整合和分类。
卷积运算的加速与优化
随着科技的不断进步,卷积运算的加速与优化问题也引起了广泛关注。为了提高卷积运算的速度和效率,研究人员提出了多种优化方法和技术手段。
- 上一篇: 揭秘“榆钱”真相:它是榆树的什么?蚂蚁庄园3月17日趣味问答
- 下一篇: 揭秘孔明灯的传奇流传之路
新锐游戏抢先玩
游戏攻略帮助你
更多+-
12/23
-
12/23
-
12/23
-
12/23
-
12/23










