如何计算三角形的高
在数学中,三角形是一种基本的几何形状,具有三条边和三个角。三角形的高是一个重要的概念,在几何学中有着广泛的应用。它不仅是计算三角形面积的基础,还在三角函数的定义、三角形的分类及性质等方面扮演着关键角色。本文将详细探讨三角形的高如何求解,包括锐角三角形、直角三角形和钝角三角形三种情况,以及如何通过公式、几何方法和向量方法求解三角形的高。
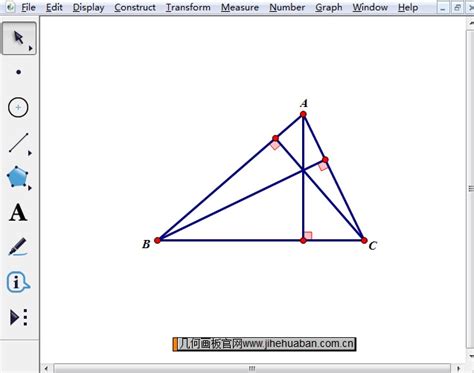
一、三角形高的定义
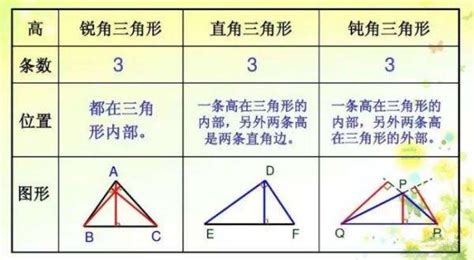
三角形的高是从三角形的一个顶点垂直于对边或对边的延长线所在的直线,交于一点的线段。这个交点称为垂足。三角形有三条高,分别对应三角形的三个顶点。在锐角三角形中,三条高都在三角形的内部;在直角三角形中,有两条高与直角边重合,另一条高是斜边上的高;在钝角三角形中,有两条高在三角形的外部。
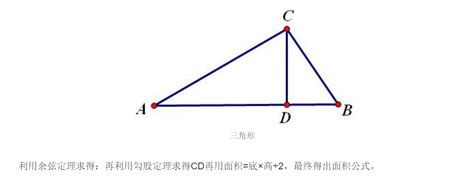
二、锐角三角形中的高
在锐角三角形中,所有的高都在三角形的内部,因此求解过程相对简单。
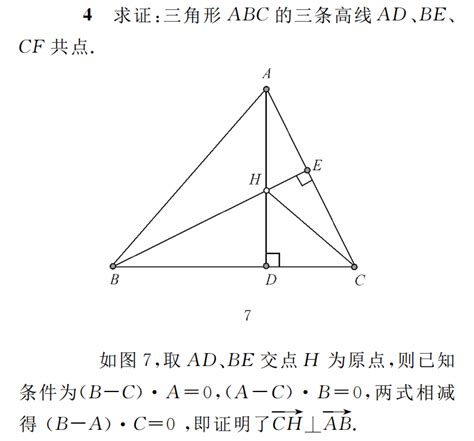
1. 公式法
给定三角形的边长a、b和c,以及对应的角A、B和C,我们可以使用三角形的面积公式来求解高。三角形面积的公式为:
S = 1/2 * 底 * 高
如果我们选择边b作为底,那么高h_b可以表示为:
h_b = (2S) / b
其中,S可以通过海伦公式或其他面积公式求得。海伦公式为:
S = √(p(p-a)(p-b)(p-c))
其中,p为半周长,即p = (a + b + c) / 2。
2. 几何方法
通过作图,我们可以直接找到三角形的高。首先,在三角形中标记一个顶点P,并选择一条边AB作为底。然后,从点P作AB的垂线,交于点D。线段PD即为三角形的高。在作图时,可以使用直尺和圆规,或者借助现代的计算工具如几何画板。
三、直角三角形中的高
在直角三角形中,高的求解有两种特殊情况:两条高与直角边重合,另一条高是斜边上的高。
1. 直角边上的高
对于直角边a和b,它们本身就是高,因为它们垂直于另外一条直角边。因此,在直角三角形中,如果我们选择直角边a作为底,那么高就是直角边b(或反之)。
2. 斜边上的高
对于斜边上的高h,我们可以使用勾股定理来求解。设直角三角形的直角边为a和b,斜边为c,斜边上的高为h。根据面积公式,我们有:
S = 1/2 * a * b = 1/2 * c * h
从中解出h,得到:
h = (a * b) / c
此外,斜边上的高h还可以通过三角函数来求解。在直角三角形中,如果角A是锐角,那么:
h = c * sin(A)
或者,如果角B是锐角,那么:
h = c * cos(B)
(因为sin(A) = cos(90° - A) = cos(B))
四、钝角三角形中的高
在钝角三角形中,有两条高在三角形的外部。因此,求解过程需要特别注意。
1. 外部高的概念
在钝角三角形中,当从钝角的顶点作高时,垂足会落在对边的延长线上。因此,这两条高被称为三角形的外部高。
2. 公式法与几何方法
对于钝角三角形,我们仍然可以使用面积公式来求解高,但是需要注意选择正确的底和高。在作图时,我们可以使用延长线的方法来找到外部高的垂足。首先,从钝角的顶点出发,作一条垂直于对边延长线的线段,交于点D(D在对边的延长线上)。线段PD即为钝角三角形的一条外部高。
3. 向量方法
向量方法提供了一种更为简洁和通用的求解三角形高的方式。设三角形的三个顶点为A、B和C,对应的向量为a、b和c(其中c = a - b,表示从B到A的向量)。如果我们要求BC边上的高(即顶点A到边BC的垂线段),可以通过向量的点积公式来求解。
首先,计算向量b和c的单位向量:
b_hat = b / |b|
c_hat = c / |c|
然后,计算向量a在向量b_hat上的投影长度。这个投影长度就是三角形的高h(注意方向):
h = |a * b_hat| = |a| * |cos(θ)|
其中,θ
- 上一篇: 揭秘:解放战争中的三大战役,它们的顺序你知道吗?
- 下一篇: 制作银行余额调节表的详细步骤
游戏攻略帮助你
更多+-
04/23
-
04/23
-
04/23
-
04/23
-
04/23













