揭秘!棱柱与棱锥的显著差异
揭秘几何世界的双胞胎:棱柱与棱锥,你真的分得清吗?
在几何学的浩瀚宇宙中,棱柱和棱锥犹如一对神秘的双胞胎,它们既相似又截然不同,共同构建着我们对空间形态的认知。今天,就让我们一起揭开它们的神秘面纱,深入探索棱柱与棱锥之间的奇妙差异,让你的几何之旅更加精彩纷呈!
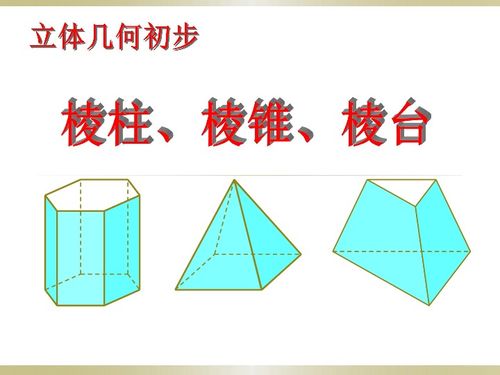
一、定义篇:初见端倪
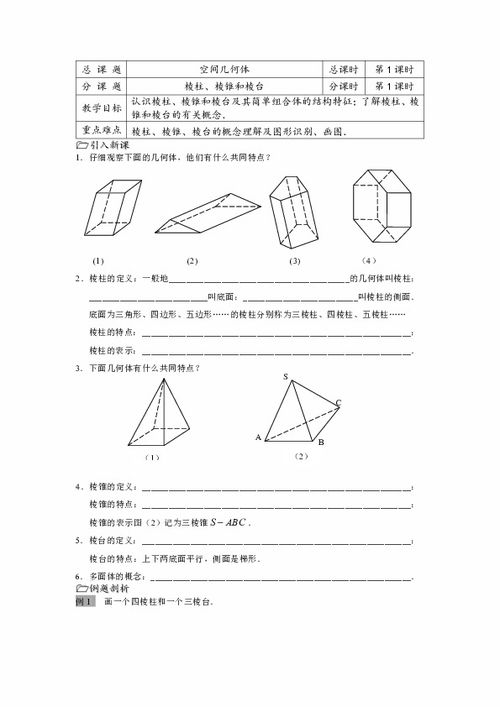
首先,让我们从定义入手,为这对双胞胎画上一幅初步的素描。棱柱,一个由两个平行且相等的多边形底面以及连接这两个底面对应顶点的侧棱面所围成的几何体。它就像是一个被拉长了的多边形,每一个侧面都是一个矩形或平行四边形,整齐划一,充满了秩序感。

而棱锥,则是由一个多边形底面及其各顶点与底面上一固定点(称为顶点)的连线所围成的几何体。它更像是一个尖锐的箭头,指向天空,底面是它的根基,而顶点则是它的灵魂所在。每一个侧面都是一个三角形,这些三角形汇聚于顶点,形成了一种向上冲刺的态势。
二、形态篇:各具特色
当我们仔细观察棱柱和棱锥的形态时,不难发现它们各自独特的魅力。棱柱以其规则的矩形或平行四边形侧面,展现出一种平稳、均衡的美感。无论是三棱柱、四棱柱(又称长方体或立方体)还是更多棱的棱柱,它们都保持着一种冷静、理性的气质,仿佛是现代建筑的缩影。
相比之下,棱锥则以其尖锐的顶点、多样的底面形状以及三角形侧面的汇聚,营造出一种动感、张力的氛围。从正三棱锥到正六棱锥,再到不规则棱锥,它们都以顶点为中心,向外辐射出强烈的视觉冲击力,就像是自然界中的山峰或火箭的尾部,充满了力量与激情。
三、性质篇:差异显著
在性质上,棱柱和棱锥的差异更是显而易见。首先,从体积上来看,棱柱的体积可以通过底面积乘以高来计算,而棱锥的体积则是等底等高的棱柱体积的三分之一。这一差异使得棱柱在存储、容纳方面更具优势,而棱锥则更擅长于表现高度、深度等立体效果。
其次,在侧面积的计算上,棱柱的侧面积等于底周长乘以高,而棱锥的侧面积则需要通过计算每一个三角形的面积再求和得到。这一差异反映了棱柱在构造上的简洁性和棱锥在构造上的复杂性。
此外,棱柱和棱锥在截面形状上也存在差异。棱柱的截面可以是平行四边形、矩形、菱形等,而棱锥的截面则更多地是三角形、椭圆等形状。这些差异使得棱柱和棱锥在应用领域上具有不同的特点和优势。
四、应用篇:各有所长
在现实生活中,棱柱和棱锥的应用无处不在,它们各自发挥着不可替代的作用。棱柱以其规则的形态和稳定的结构,成为建筑、家具、包装等领域的首选材料。从高楼大厦的框架结构到家里的书桌、椅子,再到快递包装箱,棱柱的身影无处不在。它们不仅美观大方,而且实用性强,为我们的生活带来了极大的便利。
而棱锥则以其独特的形态和动感的视觉效果,成为雕塑、装饰、玩具等领域的宠儿。从古埃及的金字塔到现代艺术雕塑,从家居装饰品到孩子们的玩具积木,棱锥都以其独特的魅力吸引着人们的目光。它们不仅丰富了我们的视觉体验,还激发了我们的创造力和想象力。
五、拓展篇:几何世界的奥秘
除了棱柱和棱锥之外,几何世界中还有许多其他奇妙的几何体等待我们去探索。例如,圆柱、圆锥、球体等,它们各自具有独特的形态和性质,共同构成了丰富多彩的几何世界。这些几何体不仅在数学、物理等学科中扮演着重要角色,还在建筑、艺术、工程等领域发挥着重要作用。
在学习几何的过程中,我们不仅要掌握各种几何体的定义、性质和计算方法,还要学会运用几何思维去解决问题。通过观察、分析、比较和归纳等方法,我们可以更好地理解和掌握几何知识,培养自己的空间想象力和逻辑思维能力。
同时,几何世界也是一个充满创意和想象的空间。我们可以通过组合、变形、缩放等手段创造出各种独特的几何造型和图案,为我们的生活增添更多的色彩和乐趣。在这个过程中,我们的创造力和审美能力也将得到不断的提升和锻炼。
六、结语:几何之美,无处不在
回顾棱柱与棱锥的奇妙之旅,我们不禁感叹几何世界的丰富多彩和无限魅力。棱柱以其规则的形态和稳定的结构展现出一种冷静、理性的美感;而棱锥则以其尖锐的顶点、多样的底面形状以及三角形侧面的汇聚营造出一种动感、张力的氛围。它们各具特色,各有所长,共同构成了几何世界的美丽画卷。
在这个充满创意和想象的时代里,让我们一起拥抱几何之美,用我们的智慧和双手去创造更多的几何奇迹吧!无论是棱柱的简洁大方
- 上一篇: 驾驶证六年期满如何换领新证
- 下一篇: 揭秘:长江全长究竟有多少千米?
火爆游戏玩不停
游戏攻略帮助你
更多+-
04/20
-
04/20
-
04/20
-
04/20
-
04/20












