轻松学会：如何画三角形的高

在我们探索几何世界的奇妙旅程中，三角形无疑是一个重要的里程碑。它不仅是几何图形的基石，更是解决许多实际问题不可或缺的工具。而在三角形的诸多性质中，“高”这一概念尤为重要，它能帮助我们深入理解三角形的结构、面积计算以及与角度的关系。那么，如何准确地在三角形中画出高呢？本文将带你一步步探索这一几何奥秘。

首先，让我们明确“三角形的高”这一概念。三角形的高是从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段就是三角形的高。这个定义听起来简单，但在实际操作时，不同类型的三角形会有不同的画法。

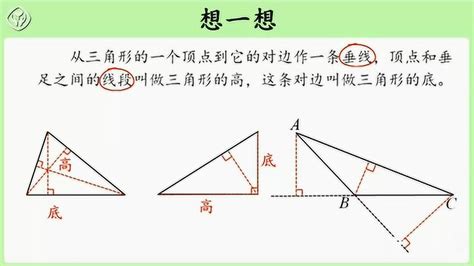
一、锐角三角形的高

锐角三角形是最直观、最易于理解的一种三角形。它的所有内角都小于90度，因此，从任何一个顶点出发，都可以轻松地向它的对边作垂线。

具体步骤如下：

1. 选择三角形的一个顶点，比如A点。

2. 使用直尺和圆规，或者直尺和铅笔（对于初学者），从A点出发，向它的对边BC（或延长线）作垂线。

3. 确保垂线与BC（或延长线）相交于一点D，那么AD就是三角形ABC的高。

在这个过程中，使用圆规可以帮助我们更精确地画出垂线。具体方法是：将圆规的一个脚固定在A点，另一个脚在BC边上移动，直到找到一个点D，使得从A点到D点的线段与BC边垂直（即，使用圆规画出的圆弧在BC边上的切点即为D点）。

二、直角三角形的高

直角三角形的高有点特殊，因为它已经包含一个90度的直角。对于直角三角形，高可以分为两种：一种是斜边上的高，另一种是两条直角边上的“高”（实际上这两条边本身就是高，因为它们垂直于另外两条边）。

斜边上的高的画法相对复杂一些：

1. 在直角三角形ABC中，假设C是直角顶点，AB是斜边。

2. 使用直尺和圆规，或者通过几何作图软件，我们可以找到斜边AB的中点D。

3. 连接中点D与直角顶点C，那么CD就是直角三角形ABC斜边上的高。

这个过程利用了直角三角形斜边上的中线等于斜边一半的性质，以及中线与对应的底边（在这里是斜边）垂直的性质。

对于直角边上的“高”，我们只需要注意它们本身就是直角边，无需额外作图。

三、钝角三角形的高

钝角三角形是三角形中最“难缠”的一种，因为它的一个内角大于90度。这导致从钝角顶点出发的高无法直接画到对边上，而需要画到对边的延长线上。

具体步骤如下：

1. 在钝角三角形ABC中，假设A是钝角顶点，BC是对边。

2. 使用直尺和圆规，从A点出发，向BC边的延长线作垂线。

3. 确保垂线与BC的延长线相交于一点D（注意D点不在三角形内部），那么AD就是三角形ABC的高。

在画钝角三角形的高时，特别需要注意的是垂足的位置。由于钝角的存在，垂足D会落在三角形的外部。这一点与锐角三角形和直角三角形的高有明显的区别。

四、特殊三角形的高

除了上述三种基本类型的三角形外，还有一些特殊类型的三角形，它们的高也有特殊的性质。

1. 等腰三角形：在等腰三角形中，两条腰相等，且底边上的两个底角也相等。在等腰三角形中画高时，可以选择底边的中点作为垂足，然后连接顶点和这个中点。这样画出的高不仅垂直于底边，还将底边平分。

2. 等边三角形：等边三角形是三条边都相等的特殊三角形。在等边三角形中，每个顶点都可以作为高的起点，而对应的底边的中点就是垂足。由于等边三角形的三条边都相等，所以它的三条高也都相等。

五、高的应用

三角形的高不仅是一个几何概念，它在解决实际问题中也有广泛的应用。

1. 面积计算：三角形的高是计算三角形面积的关键。根据三角形面积公式S=1/2×底×高，我们只需要知道三角形的底和高，就可以轻松计算出它的面积。

2. 证明问题：在几何证明中，三角形的高经常作为辅助线出现。通过巧妙地添加高，我们可以将复杂的几何问题转化为更简单的形式，从而更容易找到证明的途径。

3. 建筑设计：在建筑设计中，三角形的高也扮演着重要的角色。例如，在设计桥梁、塔楼等结构时，工程师需要考虑结构的稳定性和安全性。这时，他们往往会利用三角形的高来优化设计方案，确保结构能够承受各种外力的影响。

4. 导航定位：在导航和定位系统中，三角形的高也被广泛应用。例如，