三角形高的计算公式及方法

三角形的高计算公式是几何学中的一个基本概念，对于很多初学者来说，理解和记忆这个公式可能会有一定的挑战。然而，一旦掌握了这个公式，我们就能轻松解决与三角形高相关的问题。本文将详细介绍三角形高的计算公式，包括其推导过程、应用实例以及相关的几何性质，希望能帮助那些对三角形高计算公式感兴趣的读者更好地理解和运用这一知识点。

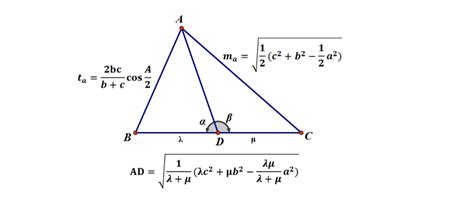
三角形的高是从一个顶点垂直到它的对边或对边的延长线所形成的线段。在三角形中，高的长度与三角形的面积和底边的长度密切相关。首先，我们来回顾一下三角形的面积计算公式：S△=1/2ah，其中a代表三角形的底边长度，h代表底边所对应的高。这个公式表明，三角形的面积是底边长度与高的乘积的一半。

基于三角形的面积公式，我们可以推导出三角形高的计算公式。将面积公式稍作变形，我们得到：h=2×S△÷a。这个公式告诉我们，如果已知三角形的面积和底边长度，就可以通过除法运算求出高的长度。

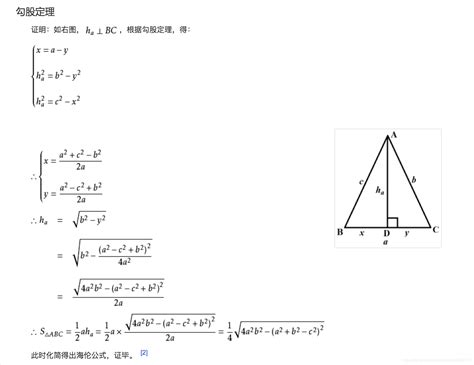
为了更好地理解三角形高的计算公式，我们可以通过一个具体的例子来进行说明。假设有一个三角形，其底边长度为8厘米，面积为24平方厘米。要求这个三角形的高，我们可以将已知数值代入到高的计算公式中：h=2×24÷8=6（厘米）。因此，这个三角形的高为6厘米。

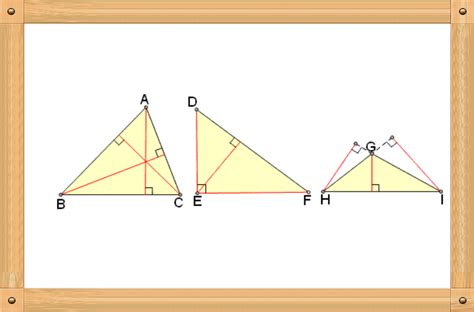
三角形高的计算公式不仅适用于普通的三角形，还适用于各种特殊类型的三角形，如直角三角形、等腰三角形和等边三角形。对于直角三角形来说，高的计算公式可以简化为直角边之一（假设为b）与斜边c之间的比值关系，即h=b×(c/a)（其中a为直角三角形的另一条直角边，但在此情境下我们实际上更常用勾股定理c²=a²+b²来间接求高）。对于等腰三角形和等边三角形，由于其具有对称性质，高的计算通常更加简便。

三角形高的计算公式的应用非常广泛。在解决实际问题时，我们经常会遇到需要计算三角形高的情况。例如，在建筑设计中，我们需要计算屋顶的倾斜角度和高度，以确保结构的稳定性和美观性；在地理测绘中，我们需要利用三角形高的概念来计算地形的高度差和坡度；在物理学中，三角形高的计算也涉及到力学、光学等多个领域。

除了三角形高的计算公式外，我们还需要了解三角形的一些基本性质。首先，三角形的内角和等于180°（内角和定理）。这一性质告诉我们，在任何一个三角形中，其三个内角的和都是固定的，即180°。这一性质在解决三角形内角问题时非常有用。

其次，三角形的外角和等于360°（外角和定理）。这一性质表明，在三角形的一个顶点处，其所有外角的和是360°。外角是三角形一个内角的补角，即与内角相邻的、在外侧的那个角。外角和定理在解决三角形外角问题时同样具有重要意义。

此外，三角形还具有一些其他重要的性质，如三角形的两边之和大于第三边（三角形的两边之和定理）、三角形的两边之差小于第三边（三角形的两边之差定理）等。这些性质在解决三角形的边长问题时非常有用，可以帮助我们判断给定的三条线段是否能够构成一个三角形。

在掌握三角形高的计算公式和性质的基础上，我们还可以进一步探讨三角形高的相关应用。例如，在解决三角形面积问题时，我们可以利用高的计算公式来求解未知量。如果已知三角形的面积和底边长度，我们可以求出高的长度；反之，如果已知三角形的高和底边长度或面积和其中一个边长，我们也可以通过计算求出另一个未知量。

此外，在解决三角形的相似和全等问题时，三角形高的概念也发挥着重要作用。相似三角形的对应边之间的比例关系是相等的，因此如果已知一个三角形的高和底边长度以及另一个相似三角形的对应边长，我们就可以通过比例关系求出另一个三角形的高。同样地，在全等三角形中，对应边和对应角都是相等的，因此如果两个三角形全等且已知其中一个三角形的高和底边长度，我们就可以直接得出另一个三角形的高。

综上所述，三角形高的计算公式是几何学中的一个重要知识点。通过掌握这个公式以及相关的几何性质和应用实例，我们可以更好地理解和运用三角形高的概念来解决实际问题。无论是在建筑设计、地理测绘还是物理学等领域中，三角形高的计算都发挥着不可替代的作用。因此，对于那些对三角形高计算公式感兴趣的读者来说，深入学习和掌握这一知识点无疑是非常有益的。