三角形周长和面积分别是什么

在数学与几何的广袤领域中，三角形作为一种基础而重要的形状，不仅承载着丰富的数学原理，还广泛渗透于我们的日常生活与自然界的众多现象之中。提及三角形，两个核心概念自然而然地跃然纸上——周长与面积。它们不仅是衡量三角形尺寸的基本尺度，更是深入理解三角形性质、解决相关问题的关键所在。本文将从定义解析、计算方法、实际应用以及几何美学等多个维度，探讨三角形的周长与面积。

一、定义解析：周长与面积的基石

周长：边界的度量

三角形的周长，简而言之，就是其三条边长度的总和。假设一个三角形有边a、b、c，则周长P可以表示为：P = a + b + c。这一简单却深刻的定义，不仅是对三角形边界长度的直接反映，也是后续诸多几何计算与证明的基础。周长概念的引入，使我们能够量化三角形的“外围尺寸”，从而在比较不同三角形大小、解决构造性问题时提供直观依据。

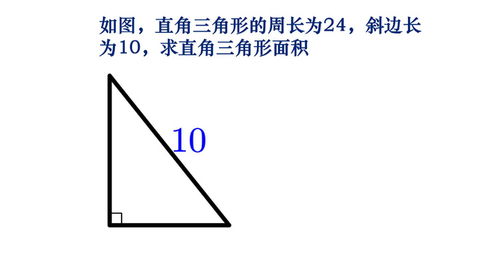
面积：空间的填充

相较于周长的线性特征，三角形的面积则代表了其内部空间的填充程度，是一个二维的量。面积的计算不仅涉及三角形的边长，往往还需考虑其高度、角度等因素。最常用的面积计算公式之一是基于底边和高度的：若三角形有一底边长为b，高为h，则其面积A为A = 0.5 × b × h。此外，利用海伦公式（Heron's formula），仅知道三角形的三边长也可求得面积，即A = √(s(s-a)(s-b)(s-c))，其中s为半周长，s = (a + b + c) / 2。

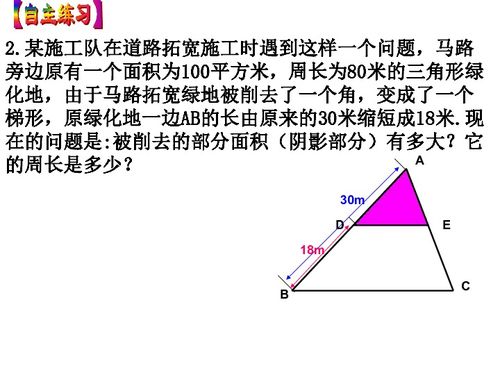
二、计算方法：从直观到抽象

直观计算：图形工具与公式

在日常教学中，对于三角形周长与面积的计算，最直接的方式是借助图形工具，如直尺测量边长，再通过简单的加法得出周长；对于面积，则可借助直角三角尺、量角器等工具确定底边与高度，进而使用公式计算。这种方法直观易懂，尤其适合初学者理解和操作。

抽象推导：解析几何与三角函数

随着数学学习的深入，我们可通过解析几何和三角函数的方法，以更抽象、更一般化的方式计算三角形的周长与面积。例如，在平面直角坐标系中，给定三角形的三个顶点坐标，利用两点间距离公式可以求出边长，进而求得周长；而对于面积，则可利用向量叉积、行列式或三角函数关系进行推导，这些方法不仅拓宽了解决问题的途径，也展示了数学内部的统一与和谐。

三、实际应用：理论与实践的桥梁

工程设计与建筑

在工程设计领域，三角形的周长与面积计算是不可或缺的技能。无论是桥梁结构的稳定性分析，还是建筑布局的空间规划，都需要精确计算三角形的相关参数。例如，在设计屋顶结构时，工程师需确保三角形支架的周长和面积满足承重与美观的双重需求，从而确保建筑的整体安全与美观。

地理测量与导航

在地理测绘与导航系统中，三角形的周长与面积计算同样扮演着重要角色。通过GPS定位技术获取的点位信息，结合三角测量原理，可以精确计算出地面区域的边界长度和面积，这对于土地规划、环境监测、灾害评估等领域具有重要意义。

计算机图形学与游戏开发

在计算机图形学与游戏开发领域，三角形的周长与面积是构建虚拟世界、实现3D渲染的基础。通过对三角形网格的精细控制，开发者能够创造出逼真的场景与角色，而周长与面积的计算则直接关系到模型的细节表现、光照效果及物理交互的逼真度。

四、几何美学：数学与艺术的交汇

几何图形的艺术表现

三角形，作为最简单的多边形之一，其周长与面积不仅承载着数学的严谨，也激发了艺术家无限的创作灵感。从古埃及金字塔的宏伟轮廓，到现代建筑中的三角形元素，周长与面积的比例关系往往成为表达设计理念、营造视觉美感的关键。

黄金分割与数学之美

特别地，当三角形的边长满足黄金分割比例时，其周长与面积之比呈现出一种难以言喻的和谐之美。黄金分割不仅在自然界中广泛存在，如海螺的生长曲线、植物叶片的排列，也是艺术作品中追求的理想比例，如达芬奇的《蒙娜丽莎》构图中的巧妙运用，展现了数学与艺术的完美融合。

结语

综上所述，三角形的周长与面积不仅是几何学中的基本概念，更是连接数学理论与实践应用的桥梁。它们不仅帮助我们量化三角形的尺寸，解决实际问题，还激发了人类对美的追求与探索。在这个过程中，我们不断挖掘数学的深层魅力，同时也深刻体会到，无论是工程的精确计算，还是艺术的抽象表达，数学都是那把开启智慧之门的钥匙，引领我们走向更加广阔的知识与审美世界。