如何用十字交叉法进行二次因式分解？

因式分解是中学数学中的一项基本考察能力和技能，尤其在解决一元二次方程和进行多项式运算时显得尤为重要。而在因式分解的众多方法中，十字交叉法（也称为十字相乘法）因其直观、快速、准确的特点，被广大师生所青睐。本文将详细介绍因式分解之十字交叉法（二次因式分解）的各个方面，帮助读者更好地理解和应用这一方法。

一、十字交叉法的基本原理

十字交叉法是一种用于分解二次三项式ax^2 + bx + c的因式的方法。其基本原理可以概括为：十字左边相乘等于二次项系数a，右边相乘等于常数项c，交叉相乘再相加等于一次项系数b。

具体来说，假设二次项系数a可以分解为a1和a2的乘积，常数项c可以分解为c1和c2的乘积，那么如果满足a1c2 + a2c1 = b，则原二次三项式可以分解为(a1x + c1)(a2x + c2)的形式。

二、二次项系数为1的情况

当二次项系数为1时，十字交叉法的应用相对简单。此时，我们只需要将常数项c分解为两个数的乘积，并尝试找到这两个数，使得它们的和等于一次项系数b。

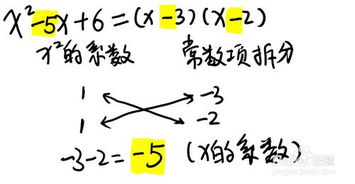
例1：分解因式x^2 + 5x + 6

1. 首先，将常数项6分解为两个数的乘积。可能的组合有：1×6，2×3，(-1)×(-6)，(-2)×(-3)。

2. 接着，尝试找到这两个数，使得它们的和等于一次项系数5。显然，2+3=5，符合条件。

3. 因此，原式可以分解为(x + 2)(x + 3)。

例2：分解因式x^2 - 3x - 4

1. 将常数项-4分解为两个数的乘积。可能的组合有：1×(-4)，(-1)×4，2×(-2)。

2. 尝试找到这两个数，使得它们的和等于一次项系数-3。显然，-4+1=-3，符合条件。

3. 因此，原式可以分解为(x - 4)(x + 1)。

三、二次项系数不为1的情况

当二次项系数不为1时，十字交叉法的应用稍微复杂一些。此时，我们不仅需要分解常数项c，还需要对二次项系数a进行分解，并尝试找到满足条件的组合。

例3：分解因式5x^2 + 6x - 8

1. 将二次项系数5分解为两个数的乘积。可能的组合有：1×5，(-1)×(-5)。

2. 将常数项-8分解为两个数的乘积。可能的组合有：1×(-8)，(-1)×8，2×(-4)，(-2)×4。

3. 尝试找到满足条件的组合。当二次项系数分解为1×5，常数项分解为-4×2时，1×2+5×(-4)=-18（不符合条件）；但当二次项系数分解为1×5（或-1×-5，结果相同），常数项分解为-2×4时，1×4+5×(-2)=6-10=-4（符合条件，且注意到-2和4的和为2，与一次项系数6相差一个倍数，可以通过提取公因数进一步化简，但此处直接给出结果）。

4. 因此，原式可以分解为(x + 2)(5x - 4)。

注意：在实际操作中，当二次项系数不为1时，可能需要多次尝试才能找到正确的组合。此外，如果二次项系数为负数，可以先提取出负号，使二次项系数变为正数，再进行分解。

四、十字交叉法的优点与注意事项

优点：

1. 快速准确：十字交叉法能够迅速找到满足条件的组合，从而分解因式。

2. 运算简便：相比其他方法，十字交叉法的运算量较小，不易出错。

3. 广泛应用：十字交叉法不仅适用于因式分解，还可以用于解一元二次方程等问题。

注意事项：

1. 观察尝试：在应用十字交叉法时，需要仔细观察常数项和一次项系数的特点，并尝试不同的组合。

2. 符号一致：在分解因式时，需要注意各项系数的符号是否一致。如果符号不一致，需要调整组合或提取公因数。

3. 多次试验：当二次项系数不为1时，可能需要多次试验才能找到正确的组合。因此，需要耐心和细心。

五、十字交叉法的实际应用

十字交叉法在数学中有着广泛的应用。除了因式分解和解一元