揭秘：轻松掌握二次函数配方成顶点式的绝妙技巧

二次函数配方成顶点式的详细步骤

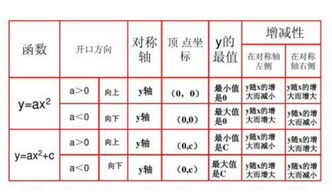
二次函数是数学中一种重要的函数形式，它的一般表达式为y=ax²+bx+c（a≠0）。而在处理二次函数问题时，我们经常需要将其转化为顶点式，即y=a(x-h)²+k的形式，以便更容易地找到函数的顶点坐标、开口方向及对称轴等关键信息。那么，如何将一般的二次函数配方成顶点式呢？以下就是详细的步骤和方法。

一、回顾二次函数的基本形式

首先，我们需要明确二次函数的一般形式y=ax²+bx+c，其中a、b、c是常数，且a≠0。这个形式也被称为二次函数的“标准式”。

二、理解顶点式的含义

顶点式y=a(x-h)²+k中的h和k分别代表二次函数图像的顶点坐标的x值和y值，而a决定了抛物线的开口方向和宽度。当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

三、配方的基本步骤

1. 提取二次项系数

在y=ax²+bx+c中，我们首先提取出二次项的系数a，得到y=a(x²+bx/a)+c。

2. 配方补全平方

接下来，我们需要对x²+bx/a进行配方，使其变为一个完全平方的形式。为此，我们需要加上和减去(b/2a)²，即y=a[x²+bx/a+(b/2a)²-(b/2a)²]+c。

这样，x²+bx/a+(b/2a)²就变成了(x+b/2a)²的完全平方形式。

3. 整理得到顶点式

最后，我们将上述表达式进行整理，得到y=a(x+b/2a)²-(b²/4a)+c。进一步合并常数项，得到y=a(x+b/2a)²+(4ac-b²)/4a。

此时，我们已经成功地将二次函数配方成了顶点式的形式，其中h=-b/2a，k=(4ac-b²)/4a。

四、通过实例加深理解

为了更好地理解上述配方过程，我们可以通过一个具体的例子来进行说明。

例：将二次函数y=2x²+4x+3配方成顶点式。

1. 提取二次项系数

首先，我们提取出二次项的系数2，得到y=2(x²+2x)+3。

2. 配方补全平方

接下来，我们对x²+2x进行配方。为了使其变为完全平方的形式，我们需要加上和减去1（因为(2/2)²=1），即y=2[x²+2x+1-1]+3。

这样，x²+2x+1就变成了(x+1)²的完全平方形式。

3. 整理得到顶点式

最后，我们将上述表达式进行整理，得到y=2(x+1)²-2+3=2(x+1)²+1。

此时，我们已经成功地将二次函数y=2x²+4x+3配方成了顶点式的形式，其中顶点坐标为(-1,1)。

五、注意事项

1. 配方过程中要确保等式两边平衡，即加上和减去的数必须相同。

2. 配方后的顶点式中的h和k可以直接读出函数的顶点坐标。

3. 配方可以帮助我们更直观地理解二次函数的性质，如开口方向、顶点位置等。

六、配方在解题中的应用

1. 求二次函数的顶点坐标

通过配方，我们可以轻松地求出二次函数的顶点坐标，即(-b/2a,(4ac-b²)/4a)。这个坐标对于分析二次函数的图像和性质非常重要。

2. 判断二次函数的开口方向

通过配方后的顶点式中的a值，我们可以判断二次函数的开口方向。当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

3. 分析二次函数的增减性

通过配方，我们还可以分析二次函数在不同区间的增减性。例如，对于开口向上的抛物线，当x<-b/2a时，函数值y随x的增大而减小；当x>-b/2a时，函数值y随x的增大而增大。反之，对于开口向下的抛物线，增减性相反。

4. 解决实际问题

在实际问题中，二次函数经常用于描述物体运动轨迹、利润最大化、成本最小化等场景。通过配方