扇形面积计算公式详解

扇形公式是几何学中一个至关重要的概念，它在计算扇形面积、弧长等几何量时起着关键作用。扇形，顾名思义，是指圆的一部分，其形状像一把展开的扇子。从几何学的角度来看，扇形公式涉及扇形的面积、弧长以及圆心角等多个维度。本文将详细介绍扇形公式的相关内容，以便读者能够深入理解并应用这些公式。

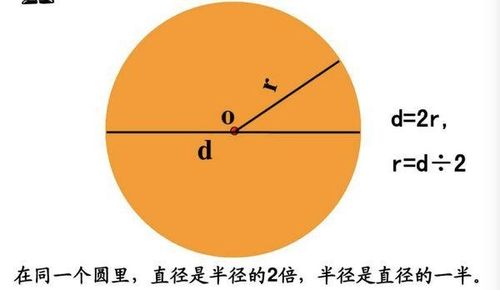
一、扇形公式的定义

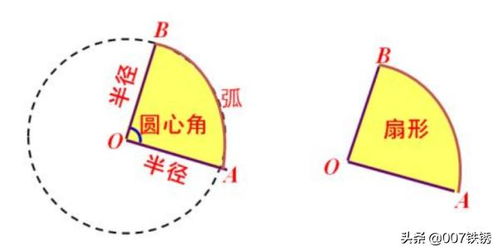
扇形公式主要用于计算扇形的面积和弧长。在圆中，扇形是由一个圆心角和它所截得的两条半径围成的部分。因此，扇形的面积和弧长与圆的半径以及扇形的圆心角密切相关。

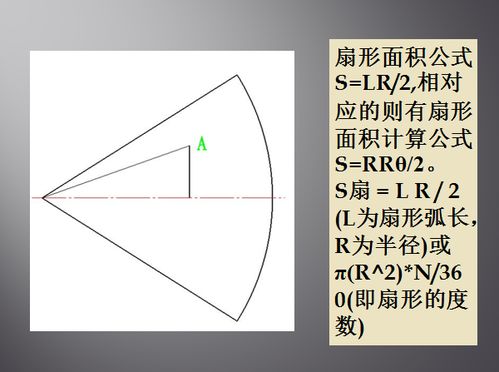
1. 扇形面积公式

扇形面积公式是扇形公式中最为基础且常用的一个。扇形面积（A）的计算公式为：

\[A = \frac{n\pi r^2}{360}\]

或者，当圆心角用弧度表示时，扇形面积公式可以简化为：

\[A = \frac{1}{2} \alpha r^2\]

其中，n 表示扇形的圆心角（以度为单位），r 表示圆的半径，α 表示扇形的圆心角（以弧度为单位）。

2. 扇形弧长公式

扇形弧长公式用于计算扇形边界上弧的长度。扇形弧长（L）的计算公式为：

\[L = \frac{n\pi r}{180}\]

或者，当圆心角用弧度表示时，扇形弧长公式可以简化为：

\[L = \alpha r\]

二、扇形公式的推导

扇形公式的推导主要基于圆的性质和几何学的基本定理。下面将分别介绍扇形面积公式和扇形弧长公式的推导过程。

1. 扇形面积公式的推导

扇形面积公式的推导可以从圆的面积公式出发。圆的面积公式为：

\[S = \pi r^2\]

扇形是圆的一部分，其面积占整个圆面积的比例等于扇形的圆心角占整个圆（360°）的比例。因此，扇形面积可以表示为：

\[A = \frac{n}{360} \times \pi r^2 = \frac{n\pi r^2}{360}\]

当圆心角用弧度表示时，扇形面积占整个圆面积的比例等于扇形的圆心角（弧度）占整个圆（2π弧度）的比例。因此，扇形面积也可以表示为：

\[A = \frac{\alpha}{2\pi} \times \pi r^2 = \frac{1}{2} \alpha r^2\]

2. 扇形弧长公式的推导

扇形弧长公式的推导可以从圆的周长公式出发。圆的周长公式为：

\[C = 2\pi r\]

扇形弧长是圆周长的一部分，其长度占整个圆周长的比例等于扇形的圆心角占整个圆（360°）的比例。因此，扇形弧长可以表示为：

\[L = \frac{n}{360} \times 2\pi r = \frac{n\pi r}{180}\]

当圆心角用弧度表示时，扇形弧长占整个圆周长的比例等于扇形的圆心角（弧度）占整个圆（2π弧度）的比例。因此，扇形弧长也可以表示为：

\[L = \frac{\alpha}{2\pi} \times 2\pi r = \alpha r\]

三、扇形公式的应用

扇形公式在几何学、工程学、物理学等多个领域都有广泛的应用。下面将介绍扇形公式在实际问题中的一些应用实例。

1. 几何学中的应用

在几何学中，扇形公式常用于计算扇形的面积和弧长。例如，在设计圆形建筑或圆形装饰物时，需要计算扇形的面积以确定所需材料的数量；在计算扇形门的开启范围时，需要计算扇形的弧长以确定门的尺寸。

2. 工程学中的应用

在工程学中，扇形公式常用于计算旋转体的表面积和体积。例如，在计算圆柱体侧面的表面积时，可以将侧面看作是一个展开后的扇形，然后利用扇形面积公式进行计算；在计算圆锥体的体积时，可以利用扇形面积公式计算圆锥底面的面积，进而求得圆锥体的体积。

3. 物理学中的应用

在物理学中，扇形公式常用于计算与圆相关的物理量。例如，在计算带电粒子在磁场中做圆周运动的轨道半径时，可以利用扇形弧长公式计算粒子在磁场中运动的弧长；在计算电磁波的波前形状时，可以利用扇形面积公式计算波前在某一时刻所占据的面积。

四、扇形公式的局限性及扩展

扇形公式虽然在大多数情况下都能满足计算需求，但在某些特殊情况下也存在局限性。