长方体和正方体的展开图具有哪些特点？

长方体和正方体作为我们日常生活中最常见的三维几何体，无论是书本、盒子还是建筑物的某些部分，都频繁出现它们的身影。而当我们试图将这些立体结构转化为平面图形，即它们的展开图时，会发现许多有趣且实用的特点。这些特点不仅能帮助我们更好地理解三维与二维空间之间的转换，还能在手工制作、包装设计等实际应用中发挥重要作用。

首先，我们先来了解一下长方体的展开图。一个长方体有六个面，分别是上面、下面、前面、后面、左面和右面。每个面都是一个矩形，而长方体的展开图就是将这六个面按照一定的顺序和方式展开到平面上。一个常见的长方体展开图布局是将上面和下面两个矩形水平放置，前面和后面两个矩形竖直放置在前后的位置，左面和右面两个矩形则填补两侧的空白。这种布局确保了每个面都能完整地展示出来，同时相邻面之间的相对位置关系也能在展开图中得到保持。

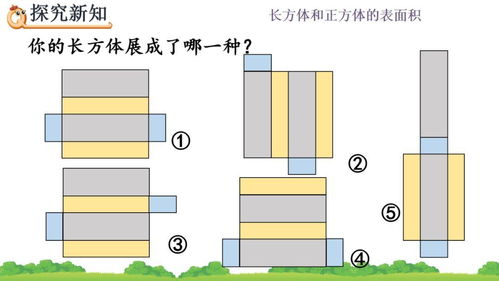
长方体的展开图有以下几个显著特点：

1. 面的连续性：在展开图中，长方体的每一个面都是相连的，没有断裂。这反映了在三维空间中，长方体的各个面是紧密相连、不可分割的。

2. 面的大小关系：由于长方体有三组相对的面大小相等（上面与下面、前面与后面、左面与右面），因此在展开图中，这些对应面的面积也是相等的。这一特点在制作纸盒等物品时尤为重要，它确保了我们可以用相同大小的纸张来覆盖所有的面。

3. 相邻面的位置关系：在展开图中，相邻面的位置关系得到了明确的表示。例如，在常见的布局中，上面与前面、上面与左面、下面与后面、下面与右面是相邻的。这种位置关系对于后续的折叠和组装步骤至关重要。

4. 灵活性：虽然长方体展开图有常见的布局方式，但实际上它的展开方式并不唯一。通过改变面的排列顺序和相对位置，我们可以得到多种不同的展开图。这种灵活性为我们提供了更多的创意空间，尤其是在设计包装盒和广告海报时。

接下来，我们再来看看正方体的展开图。正方体是长方体的一个特例，它的六个面都是正方形，且所有棱的长度都相等。因此，正方体的展开图也具有一些独特的特点。

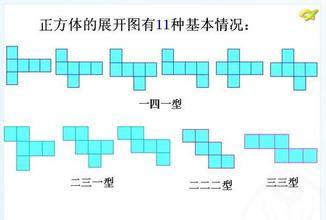
正方体的展开图通常有以下几种常见的布局方式：

“1-4-1”型：这种布局方式将一个正方形放在中间，上下各放两个正方形，左右两侧各放一个正方形。这种布局方式清晰明了，易于理解和记忆。

“2-3-1”型：这种布局方式将两个正方形并排放置在中间位置，上面放一个正方形，下面放三个正方形（其中两个相连，另一个单独放置）。这种布局方式相对复杂一些，但也能很好地展示正方体的结构特点。

“3-3”型：这种布局方式将六个正方形分为两组，每组三个正方形相连，然后上下放置。这种布局方式在视觉上更加紧凑和对称。

正方体的展开图具有以下特点：

1. 面的均等性：由于正方体的六个面都是正方形且大小相等，因此在展开图中，每个面的面积都是相同的。这一特点使得正方体的展开图在视觉上更加均衡和协调。

2. 边的等长性：正方体的所有棱的长度都相等，这一特点在展开图中也得到了体现。无论是相邻边还是相对边，在展开图中都保持了相等的长度。这为我们判断正方体的形状和大小提供了重要的依据。

3. 展开方式的多样性：与长方体类似，正方体的展开方式也不唯一。虽然常见的布局方式只有几种，但通过旋转、翻转等操作，我们可以得到更多不同的展开图。这种多样性为我们提供了更多的选择和创意空间。

4. 相邻面的位置关系：在正方体的展开图中，相邻面的位置关系也得到了明确的表示。虽然正方体的每个面都可以与其他任意面相邻，但在展开图中，这种相邻关系被固定下来了。这为我们后续的折叠和组装步骤提供了明确的指导。

在实际应用中，长方体和正方体的展开图具有广泛的应用价值。例如，在包装设计中，我们需要根据产品的形状和大小来设计合适的包装盒。通过绘制长方体的展开图，我们可以准确地计算出包装盒所需纸张的大小和形状，从而确保包装盒的完整性和美观性。此外，在手工制作中，我们也经常需要用到长方体和正方体的展开图。通过将这些立体结构转化为平面图形，我们可以更加方便地进行裁剪、折叠和组装等操作。

同时，长方体和正方体的展开图还具有重要的教育意义。通过学习这些展开图的特点和绘制方法，我们可以更好地理解三维空间与二维空间之间的转换关系。这对于培养学生的空间想象力和几何直觉具有重要的作用。

总之，长方体和正方体的展开图具有许多有趣且实用的特点。这些特点不仅帮助我们更好地理解这些立体结构的结构和性质，还能在实际应用中发挥重要的作用。通过学习和掌握这些特点，我们可以更加灵活地运用长方体和正方