余切函数图像特性解析

余切函数的图像和性质

余切函数是三角函数中的一种，在数学和工程领域有着广泛的应用。本文将详细介绍余切函数的图像和性质，帮助读者全面理解这一概念。

一、余切函数的定义

余切函数，记作cotx，定义为任意实数x（x≠kπ，k为整数）对应的角的余切值。具体地说，如果角x（以弧度为单位）的终边经过点P(x, y)（x≠0），则cotx = y/x。值得注意的是，余切函数与正切函数存在密切关系，cotx = 1/tanx。此外，在直角三角形中，余切函数可以理解为邻边长度与对边长度的比值。

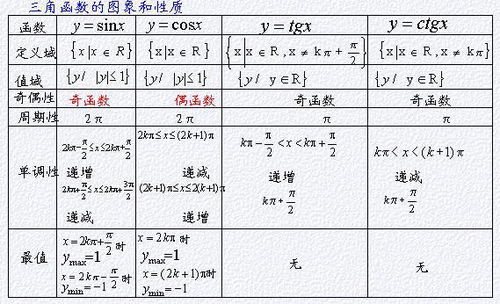
二、余切函数的图像

余切函数的图像，也称作余切曲线，是由一系列相互平行的直线x=kπ（k∈Z）隔开的无穷多支曲线组成的。这些曲线在每一个开区间(kπ, (k+1)π)上都是减函数，并且由于余切函数的周期性，图像的每一部分在横轴上相隔π个单位后重复出现。

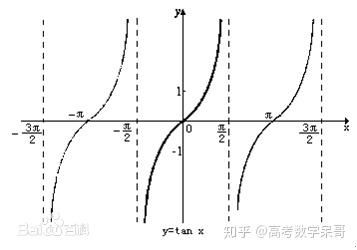
要画出余切函数的图像，可以先考虑正切函数的图像。将正切函数图像向左平移π/2个单位，然后将得到的图像绕点(kπ/2 + π/4, 0)旋转180度，即可得到余切函数的图像。这是因为cotx = tan(-x + π/2)，这显示了余切函数和正切函数之间的紧密联系。

三、余切函数的性质

1. 定义域和值域

余切函数的定义域为{x|x≠kπ, k∈Z}，即所有使得分母不为零的x值。这是因为当x=kπ时，tanx不存在，从而cotx也不存在。余切函数的值域为全体实数集R，即它可以取任意实数值。

2. 奇偶性

余切函数是奇函数，这可以由诱导公式cot(-x) = -cotx推出。奇函数的图像关于原点对称，因此余切函数的图像也关于原点(0,0)对称，但由于余切函数的定义域中不包含使分母为零的点，这一对称性在图像上表现为关于点(kπ/2, 0)（k∈Z）的中心对称。

3. 周期性

余切函数是周期函数，周期为kπ（k∈Z且k≠0），最小正周期T=π。这意味着余切函数的图像在每一个长度为π的区间上都是相似的，并且不断重复。这一周期性在应用中非常有用，可以帮助我们简化复杂的问题。

4. 单调性

在每一个开区间(kπ, (k+1)π)（k∈Z）上，余切函数都是减函数。这是因为在这个区间内，随着x的增大，tanx的值从负无穷增大到正无穷，而cotx = 1/tanx，因此cotx的值从负无穷减小到正无穷。然而，在整个定义域上，余切函数不具有单调性。

5. 对称性

余切函数关于点(kπ/2, 0)（k∈Z）中心对称。这是因为当x=kπ/2时，cotx=0，并且由于余切函数的周期性，这一对称性在每个周期内的相应点上重复出现。这种对称性使得余切函数的图像具有一种规则而美丽的结构。

四、余切函数的应用

余切函数在三角学、工程学、物理学等领域有着广泛的应用。例如，在解决与角度相关的问题时，余切函数可以帮助我们找到角度的余切值，从而确定角度的大小。在工程学中，余切函数常用于设计和分析各种机械结构，如齿轮、传动轴等。在物理学中，余切函数在波动、振动等现象的分析中也发挥着重要作用。

五、余切函数与反函数

反函数是数学中的一个重要概念，它是指如果一个函数f的对应法则为y=f(x)，则它的反函数f⁻¹的对应法则为x=f⁻¹(y)。对于余切函数cotx，其反函数可以表示为x=arccot(y)。然而，由于余切函数的值域为全体实数集R，而反余切函数arccot(y)的定义域也为R，但值域为(0, π)且不包括π/2，因此反余切函数在应用中需要注意其定义域和值域的限制。

六、结论

余切函数作为三角函数中的一种，具有独特的图像和性质。通过对其定义、图像、性质以及应用的全面介绍，我们可以更好地理解和应用这一概念。余切函数的图像由