扇形面积及弧长计算公式详解
扇形是圆的一个重要组成部分,它在几何学、工程学、物理学以及日常生活中都有着广泛的应用。当我们想要计算扇形的面积或者弧长时,就需要用到扇形公式。那么,扇形公式是什么呢?让我们一起深入探究。
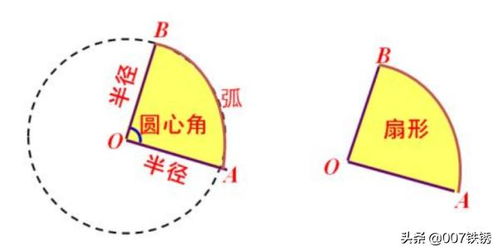
首先,我们要明确什么是扇形。扇形是由圆心角的两条半径和圆上的一段弧围成的图形。如果我们把一个完整的圆看作360度,那么扇形所占的角度就是这个圆心角,通常用θ(theta)来表示,单位是度或者弧度。
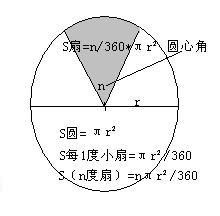
扇形面积的公式
扇形面积的计算公式是扇形学习中最重要的部分之一。扇形面积公式为:
扇形面积 = (θ/360) × π × r²
这里的θ是圆心角的度数,π是一个数学常数,约等于3.14159,r是圆的半径。
这个公式的来源可以这样理解:扇形的面积占整个圆面积的比例,就等于圆心角占整个圆的角度(360度)的比例。所以,如果我们知道整个圆的面积(π × r²),然后乘以圆心角占的比例(θ/360),就可以得到扇形的面积了。
扇形弧长的公式
除了面积,扇形弧长也是常见的计算需求。扇形弧长公式为:
扇形弧长 = (θ/360) × 2π × r
这里的θ同样是圆心角的度数,π是数学常数,r是圆的半径。
这个公式的推导基于圆的周长公式(2πr),扇形弧长占整个圆周长的比例等于圆心角占整个圆的角度的比例。因此,我们只需要将圆的周长乘以这个比例,就可以得到扇形的弧长了。
使用扇形公式的实例
为了更好地理解扇形公式,我们可以通过一些实例来进行计算。
实例一:计算扇形面积
假设有一个半径为5厘米的圆,扇形的圆心角为90度。我们要求这个扇形的面积。
根据扇形面积公式:
扇形面积 = (θ/360) × π × r²
将已知数值代入公式:
扇形面积 = (90/360) × π × 5² = (1/4) × π × 25 ≈ 19.63 平方厘米
所以,这个扇形的面积大约是19.63平方厘米。
实例二:计算扇形弧长
同样地,我们用这个半径为5厘米的圆,扇形的圆心角为90度。这次我们要求这个扇形的弧长。
根据扇形弧长公式:
扇形弧长 = (θ/360) × 2π × r
将已知数值代入公式:
扇形弧长 = (90/360) × 2π × 5 = (1/4) × 2π × 5 = (1/2) × π × 5 ≈ 7.85 厘米
所以,这个扇形的弧长大约是7.85厘米。
扇形公式的进一步理解
扇形公式的应用不仅仅局限于直接计算面积和弧长,它们还可以用于推导其他几何量,以及解决更复杂的问题。
扇形与三角形的关系
在某些情况下,扇形可以与三角形进行关联。例如,当我们知道扇形的面积和半径时,可以通过公式反推出圆心角的大小。同样地,如果我们知道扇形的弧长和半径,也可以求出圆心角。
扇形公式的推广
扇形公式还可以推广到更复杂的几何形状,如圆环扇(环形的一部分)、椭圆扇等。这些推广的公式虽然形式更加复杂,但基本原理仍然与扇形公式相同,即通过几何形状占整个形状的比例来计算所需的几何量。
扇形公式的实际应用
扇形公式在现实生活中的应用非常广泛。以下是一些常见的应用场景:
1. 工程学:在建筑和机械设计中,扇形常用于表示圆柱体的侧面展开图、齿轮的啮合部分等。通过扇形公式,工程师可以准确地计算出这些部分的面积和弧长,从而设计出合理的结构。
2. 物理学:在物理学中,扇形经常用于描述角动量、角速度等物理量的分布。扇形公式可以帮助物理学家计算这些物理量的大小和方向。
3. 天文学:在天文学中,扇形可以用来表示星系、行星轨道等天体运动的轨迹。通过扇形公式,天文学家可以计算出这些轨迹的面积和弧长,从而分析天体的运动规律。
4. 日常生活:在日常生活中,扇形也无处不在。例如,我们在切蛋糕时,通常会把蛋糕切成扇形块;在制作扇形窗花、扇形装饰品时,也需要用到扇形公式来计算所需的材料大小。
结论
扇形公式是计算扇形面积和弧长的基本工具,它们在几何学、工程学、物理学以及日常生活中都有着广泛的应用。通过理解扇形公式的来源和推导过程,我们可以
- 上一篇: 三阶魔方初学者入门指南
- 下一篇: 打造超萌手帐,简单漂亮一键get!
新锐游戏抢先玩
游戏攻略帮助你
更多+-
11/27
-
11/27
-
11/27
-
11/27
-
11/27






