等腰梯形面积的计算方法

等腰梯形的面积求解

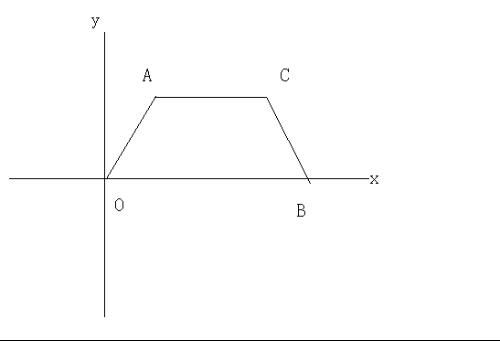
等腰梯形是几何学中的一个重要图形，其独特的性质使得在计算面积时相对简便。本文将详细介绍等腰梯形的定义、性质以及面积的计算方法，并通过具体例子来展示如何求解等腰梯形的面积。

等腰梯形是指一组对边平行且另一组对边（腰）相等的四边形。设等腰梯形的上底为a，下底为b，高为h，腰为l。为了直观理解，我们可以想象一个等腰梯形，它的上底和下底是平行的线段，长度分别为a和b，而两侧腰的长度均为l，高h是从上底到下底的垂直距离。

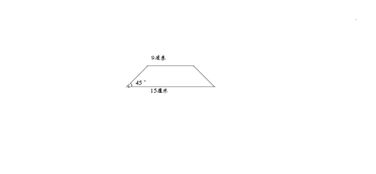
等腰梯形具有以下几个重要性质：

1. 两条腰相等，即l=l（自反性）。

2. 等腰梯形在同一底上的两个底角相等。具体来说，如果我们延长上底和下底，使它们相交于一点，那么从这一点到梯形两腰的夹角是相等的。

3. 等腰梯形的对角线相等。设等腰梯形的对角线分别为d1和d2，则d1=d2。

4. 等腰梯形是轴对称图形，对称轴是经过上底和下底中点的直线。

基于等腰梯形的性质，我们可以推导出其面积的计算公式。等腰梯形的面积计算公式为：

面积S = (上底 + 下底) × 高 ÷ 2

即：

S = (a + b) × h ÷ 2

这个公式与平行四边形的面积公式类似，只是需要将上底和下底相加后再乘以高的一半。这个公式简洁明了，是求解等腰梯形面积的直接方法。

接下来，我们通过几个具体例子来展示如何运用这个公式求解等腰梯形的面积。

例1：已知等腰梯形的上底为5厘米，下底为10厘米，高为6厘米，求面积。

根据等腰梯形的面积公式，我们有：

面积S = (5 + 10) × 6 ÷ 2

= 15 × 6 ÷ 2

= 90 ÷ 2

= 45（平方厘米）

所以，这个等腰梯形的面积是45平方厘米。

例2：已知等腰梯形的上底为8米，腰为10米，高为7.5米，求面积和下底长度。

首先，我们求解面积。由于题目没有直接给出下底的长度，但我们可以用面积公式来求解。不过，为了完整性，我们会在求解面积后，再回头求下底的长度。

面积S = (8 + b) × 7.5 ÷ 2

由于我们现在不知道下底b的长度，我们可以暂时用S表示面积，先保留这个公式。但题目中给出了腰的长度为10米，我们可以利用勾股定理来求解下底的长度。

在等腰梯形中，如果我们从上底的一个端点做一条垂直于下底的线段（即高），那么会形成一个直角三角形。这个直角三角形的直角边分别是等腰梯形的高和上下底之差的一半，斜边是等腰梯形的腰。

设上下底之差的一半为x，则：

x = (b - 8) ÷ 2

根据勾股定理，我们有：

x² + h² = l²

代入已知的h=7.5和l=10，我们得到：

x² + 7.5² = 10²

x² + 56.25 = 100

x² = 43.75

x = √43.75 ≈ 6.61（米）（取正值，因为长度不能为负）

所以，下底b的长度为：

b = 8 + 2x

= 8 + 2 × 6.61

= 8 + 13.22

= 21.22（米）

现在我们可以求解面积了：

面积S = (8 + 21.22) × 7.5 ÷ 2

= 29.22 × 7.5 ÷ 2

= 219.15 ÷ 2

= 109.575（平方米）

为了简化，我们可以将其四舍五入到小数点后两位：

S ≈ 109.58（平方米）

所以，这个等腰梯形的面积是109.58平方米，下底长度是21.22米。

例3：已知等腰梯形的面积为120平方厘米，高为8厘米，求上底和下底之和。

根据等腰梯形的面积公式，我们有：

120 = (a + b) × 8