椭圆公式是什么？

椭圆，这一数学领域中的经典几何形状，自古以来便与人类的认识和探索紧密相连。它不仅是自然界中许多现象的抽象表现，如行星轨道、天体运行路径，也是现代工程技术、物理学、美学设计等多个领域不可或缺的基本元素。椭圆的魅力，在于其简约而不简单的数学公式背后，蕴含着丰富的数学之美、物理之韵与应用之广。

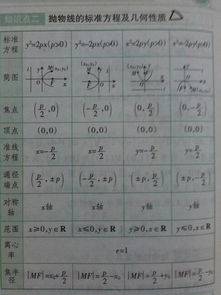
椭圆的数学定义与公式

椭圆的定义基于平面上两点（焦点）与一点（动点）之间的距离之和为常数这一核心概念。具体而言，椭圆可以被描述为平面上所有点P的集合，这些点到两个固定点F1和F2（焦点）的距离之和等于一个大于F1和F2之间距离的常数2a（长轴长）。数学公式表示为：PF1 + PF2 = 2a。此外，从椭圆的中心O到椭圆上任一点的距离r随着角度θ的变化而变化，形成椭圆的参数方程：x = a·cosθ, y = b·sinθ，其中a为长半轴，b为短半轴，且c² = a² - b²，c为焦点到中心的距离。

几何视角下的椭圆

在几何学中，椭圆是一种完美的对称图形，它不仅拥有两条相互垂直的对称轴（长轴和短轴），还呈现出镜面对称和旋转对称的双重特性。这种对称美，使得椭圆在建筑设计、艺术创作中常常被用作象征和谐与平衡的元素。例如，古罗马的万神庙、现代的天文台穹顶等，都巧妙地运用了椭圆的形态，赋予建筑以独特的视觉效果和深远的意义。

物理学中的椭圆轨道

在物理学领域，特别是天体力学中，椭圆成为描述行星、卫星等天体绕中心天体运动路径的精确模型。开普勒第一定律指出，行星绕太阳运行的轨道是一个椭圆，太阳位于椭圆的一个焦点上。这一发现彻底改变了人类对宇宙的认识，奠定了经典力学的基础。利用椭圆的数学公式，科学家们能够精确计算行星的位置、速度以及它们与太阳之间的引力关系，从而预测天文现象，如彗星回归、行星冲日等。此外，在人造卫星、宇宙飞船的轨道设计中，椭圆轨道的理论也发挥着至关重要的作用，帮助人类实现太空探索的梦想。

工程学中的椭圆应用

椭圆在工程学和制造业中的应用同样广泛。从机械设计中的凸轮轮廓、连杆机构，到精密光学元件的制造，椭圆曲线都是不可或缺的。例如，在机械设计中，通过精心设计的椭圆凸轮，可以实现更加平滑、高效的动力传输，减少磨损和振动；在光学领域，椭球面镜能够有效地收集和平行化光线，广泛应用于天文望远镜、激光器和光学传感器中，提高了光学系统的性能和精度。此外，在无线通信、数据传输等领域，椭圆曲线密码学作为一种先进的加密技术，因其高效、安全的特点而被广泛采用，保护着信息时代的数据安全。

艺术与审美中的椭圆

椭圆不仅是科学和工程的宠儿，在艺术领域同样占据一席之地。从文艺复兴时期的画作到现代设计的图案，椭圆形态因其流畅、和谐的线条而受到艺术家们的青睐。达·芬奇的《蒙娜丽莎》中，背景的远山以微妙的椭圆形态融入画面，增强了作品的深邃感和神秘氛围。在现代平面设计和广告中，椭圆常被用作强调信息、引导视线的设计元素，创造出视觉上的和谐与统一。椭圆还与人类的身体美学紧密相关，如女性的胸部轮廓、面部轮廓等，常常被描绘成椭圆形，传达出优雅与柔和的审美信息。

日常生活与椭圆

椭圆的身影同样遍布我们的日常生活。从篮球场、足球场的场地布局，到体育馆内椭圆形的跑道设计，都遵循着椭圆提供的最佳路径和最优效率原则。在运动器材中，椭圆机作为一种流行的健身设备，模拟了步行、跑步时的自然动作，以其低冲击、全身运动的特点，受到广大健身爱好者的喜爱。此外，在日常用品中，椭圆形的碗、盘子等餐具，不仅便于拿取和使用，还能增加餐桌的美感，展现出生活中的艺术与实用性并存。

数学深探：椭圆的几何变换与性质

在数学更深层次的探索中，椭圆与其他几何图形的关系及其变换性质也是研究的热点。通过仿射变换、投影变换等手段，椭圆可以转化为其他几何形状，如圆、抛物线、双曲线等，这一过程揭示了不同几何形状之间的内在联系和统一美。椭圆的焦点、准线、切线等性质，更是解析几何、微分几何研究的重要课题，为解决复杂数学问题提供了强有力的工具。

结语

综上所述，椭圆作为一个看似简单的几何形状，却承载着丰富的数学原理、物理规律、工程技术和艺术美学。它不仅是科学家研究的对象，艺术家创作的灵感，更是连接自然科学与人文艺术的桥梁。通过椭圆的公式，我们得以窥见一个既古老又现代、既理论又实践、既微观又宏观的奇妙世界。椭圆，以它独有的