揭秘：对称图形与轴对称图形的核心差异

在数学的世界中，对称图形与轴对称图形是两个既相似又存在显著差异的概念。它们都是图形美学的重要组成部分，不仅在数学学习中占据重要地位，还广泛应用于建筑、艺术、物理等多个领域。本文将从定义、性质、识别方法以及实例分析等方面，深入探讨对称图形与轴对称图形的区别。

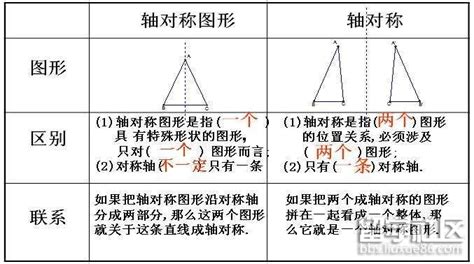
首先，我们需要明确对称图形的广义定义。对称图形指的是一个图形关于某条直线、某个点或某个平面具有某种不变性。即，当图形沿这条直线折叠、绕这个点旋转或相对于这个平面进行某种操作时，图形的某部分能够与另一部分完全重合。这种性质使得对称图形在视觉上呈现出一种平衡、和谐的美感。

接下来，我们详细解析轴对称图形的定义与性质。轴对称图形是指一个图形关于某条直线（称为对称轴）具有对称性。具体而言，如果沿着对称轴将图形折叠，图形的两侧能够完全重合。这种对称性的核心在于对称轴的存在，它像一把无形的尺子，衡量着图形两侧的平衡与一致。轴对称图形的性质包括：对称轴两侧的图形完全相同，即形状、大小、方向均保持一致；对称轴可以是任意方向，包括水平、垂直、倾斜等；在轴对称图形中，对称轴两侧的对应点距离对称轴的距离相等，且连线垂直于对称轴。

为了更直观地理解轴对称图形，我们可以通过一些实例进行说明。例如，正方形、长方形、等腰三角形、等腰梯形等都是典型的轴对称图形。以正方形为例，其有四条对称轴，分别是两条对角线以及连接正方形对边中点的两条直线。沿着这些对称轴折叠正方形，其两侧均能完全重合。

然而，对称图形并不仅限于轴对称这一种形式。除了轴对称外，还有中心对称（或点对称）和平面对称（或镜像对称）等其他类型的对称。中心对称图形指的是一个图形关于某一点（称为对称中心）具有对称性。如果绕这个点旋转180度，图形的每一部分都能与另一部分完全重合。平面对称图形则是关于某个平面（如镜子）具有对称性，当图形相对于这个平面进行反射时，其像与原图能够完全重合。

现在，我们来对比轴对称图形与其他类型对称图形的区别。首先，在识别方法上，轴对称图形主要依赖于对称轴的存在与确定。而中心对称图形则需要找到对称中心，并验证图形绕该点旋转180度后的重合性。平面对称图形的识别则涉及到一个平面的选择与图形相对于该平面的反射效果。其次，在性质上，轴对称图形的对称轴是直线，而中心对称图形的对称中心是点，平面对称图形的对称则是基于一个平面。这些差异导致了不同类型的对称图形在视觉表现和应用场景上的不同。

进一步地，我们可以从图形的构成元素来分析这些差异。轴对称图形的构成通常基于对称轴的两侧具有相同的结构、形状和大小。而中心对称图形则强调图形相对于对称中心的旋转对称性，即图形的每一部分都能绕对称中心旋转到另一个对应的位置。平面对称图形则关注图形相对于对称平面的镜像关系，即图形的每一部分都能在对称平面中找到一个对应的镜像部分。

此外，对称图形在数学中具有重要的应用价值。在几何学中，对称性是图形分类和性质研究的重要依据。在代数中，对称图形与对称群、对称多项式等数学概念紧密相连。在物理学中，对称性原理是解释自然现象、推导物理定律的重要工具。例如，在晶体学中，晶体的对称性决定了其物理性质和化学性质。在生物学中，对称性也是生物体形态和功能的重要特征之一。

在实际应用中，对称图形的价值同样不可忽视。在建筑设计中，对称布局能够营造出庄重、稳定的视觉效果，增强建筑物的整体美感。在艺术创作中，对称图形被广泛应用于图案设计、雕塑创作等领域，以展现艺术家的审美追求和创作技巧。在计算机图形学中，对称图形的生成与处理技术是计算机图形渲染、动画制作等关键技术之一。

综上所述，对称图形与轴对称图形在数学中既相互联系又各具特色。轴对称图形作为对称图形的一种重要类型，在定义、性质、识别方法以及实例分析等方面都表现出独特的特点。而其他类型的对称图形，如中心对称图形和平面对称图形，则在视觉表现和应用场景上呈现出不同的优势和魅力。通过对这些对称图形的深入学习和理解，我们可以更好地把握数学中的对称美，将其应用于实际生活和科学研究中，推动人类文明的进步与发展。