揭秘梯形面积的计算奥秘

在计算几何学中，梯形面积的计算是一个基础且实用的知识点。梯形，作为一种四边形，具有一对平行的对边，这对平行的边被称为梯形的上底和下底，而另外两条边则被称为梯形的腰。了解梯形面积的计算方法，对于日常生活和工程应用都具有重要意义。

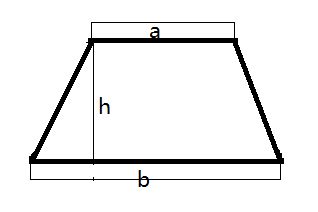
首先，我们需要明确梯形面积的计算公式。梯形面积的计算公式是：面积 = (上底 + 下底) × 高 ÷ 2。这个公式看似简单，但却蕴含了丰富的几何原理。其中，“上底”指的是梯形较短的那条平行边，“下底”是梯形较长的那条平行边，而“高”则是从上底到下底的垂直距离。

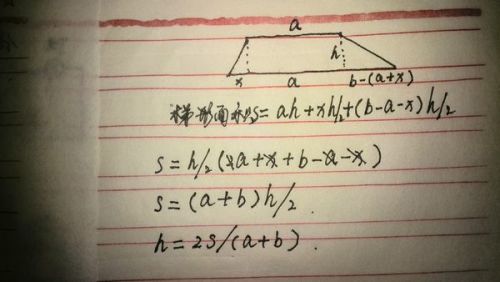
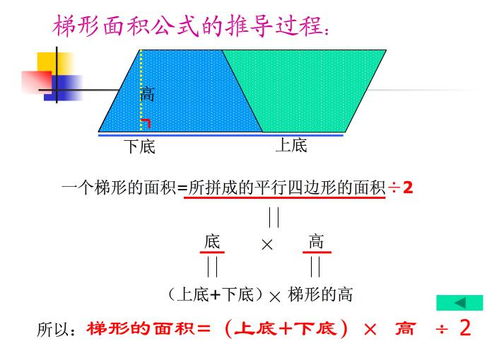
为了更直观地理解这个公式，我们可以借助图形来进行说明。想象一个梯形，它的上底是a，下底是b，高是h。如果我们把这个梯形分成两个小部分，一个是上底为a、高为h的小矩形，另一个是两边分别为a、b和高为h的直角三角形组成的三角形区域，然后通过平移三角形的部分，使其与矩形的另一侧组成一个大的矩形。此时，这个“大矩形”的长边并不是真正的梯形下底b，而是上底a与下底b之和的一半，即(a+b)/2，而宽则是梯形的高h。因此，整个梯形的面积就等于这个大矩形的面积，即(a+b)/2 × h，简化后就是梯形面积的公式：(上底 + 下底) × 高 ÷ 2。

接下来，我们通过一些实例来具体说明如何运用这个公式计算梯形面积。

实例一：已知梯形的上底是3米，下底是5米，高是2米。将这些值代入梯形面积的公式，我们得到：面积 = (3 + 5) × 2 ÷ 2 = 8平方米。这个计算过程非常直观，只需将上底和下底相加，然后乘以高，最后再除以2即可。

实例二：在实际应用中，梯形面积的计算往往更加复杂。比如，我们可能需要计算一个不规则形状的池塘的面积，而这个池塘的形状近似于梯形。在这种情况下，我们需要先通过测量或估算得到梯形的上底、下底和高的值，然后再使用梯形面积的公式进行计算。假设我们测得池塘的上底是10米，下底是15米，由于池塘的形状不规则，高的值可能需要通过多次测量并取平均值来得到，假设最终测得的高是3米。将这些值代入梯形面积的公式，我们得到：面积 = (10 + 15) × 3 ÷ 2 = 37.5平方米。虽然这个计算过程比第一个实例复杂一些，但原理是相同的。

此外，梯形面积的计算还有一些变种和扩展应用。比如，在计算梯形的表面积时，如果梯形是三维形状（如梯形棱柱）的一部分，我们可能需要计算多个梯形的面积之和，并将它们相加得到整个形状的表面积。又比如，在计算梯形的体积时，如果梯形是三维形状（如梯形台体）的底面，我们需要先计算梯形的面积，然后再乘以梯形台体的高来得到体积。这些变种和扩展应用虽然增加了计算的复杂性，但也展示了梯形面积计算在几何学和工程学中的广泛应用。

在实际应用中，梯形面积的计算还常常与其他几何形状的面积计算相结合。比如，在计算不规则多边形的面积时，我们可能会将其分割成多个梯形、三角形或矩形等简单形状，然后分别计算它们的面积，并将这些面积相加得到整个多边形的面积。这种方法虽然需要一些技巧和经验，但它是解决复杂几何形状面积计算问题的有效手段之一。

为了提高梯形面积计算的准确性和效率，我们还可以借助一些工具和方法。比如，我们可以使用测量工具（如卷尺、激光测距仪等）来精确测量梯形的上底、下底和高的值；我们可以使用计算器来进行复杂的数学运算；我们还可以使用计算机图形软件来绘制梯形并计算其面积。这些工具和方法不仅可以提高计算的准确性，还可以简化计算过程，使梯形面积的计算更加方便快捷。

综上所述，梯形面积的计算是一个基础且实用的几何知识点。通过掌握梯形面积的计算公式和方法，我们可以解决许多与梯形相关的几何问题。同时，通过与其他几何形状的面积计算相结合，我们还可以解决更加复杂的几何问题。因此，无论是在日常生活还是工程应用中，梯形面积的计算都具有重要的意义和价值。

最后需要强调的是，虽然梯形面积的计算看似简单，但在实际应用中却需要注意一些细节和技巧。比如，在测量梯形的尺寸时需要注意测量的准确性和精度；在计算面积时需要注意运算的顺序和结果的取整；在解决复杂问题时需要注意将问题分解成多个简单问题进行求解等。只有掌握了这些细节和技巧，我们才能更好地应用梯形面积的计算方法来解决实际问题。