揭秘等腰三角形：神奇三线合一的奥秘

等腰三角形是数学中一个重要的几何形状，其独特的性质使得它在几何证明和问题解决中扮演着关键角色。在众多性质中，“三线合一”是等腰三角形独有的一个显著特征，也是许多几何证明题中的核心要素。那么，等腰三角形的“三线合一”究竟是哪三线呢？让我们深入探讨一下。

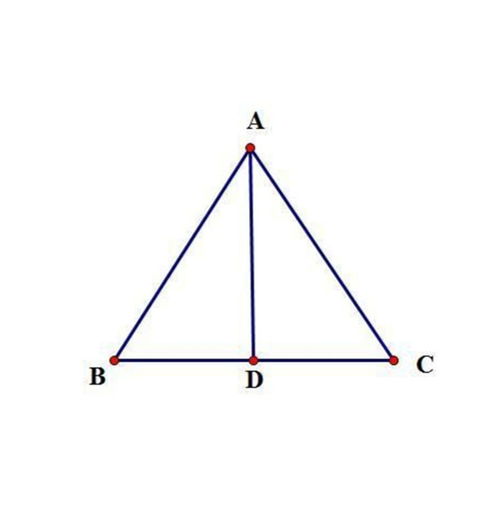
首先，我们需要明确等腰三角形的定义。等腰三角形是指至少有两边相等的三角形，其中相等的两条边被称为这个三角形的腰，另一边则被称为底边。两腰之间的夹角被称为顶角，而腰与底边之间的夹角则被称为底角。值得注意的是，等腰三角形的两个底角度数是相等的，这是等腰三角形的一个重要性质。

当我们谈论等腰三角形的“三线合一”时，我们指的是在等腰三角形中，顶角的角平分线、底边上的中线以及底边上的高线这三条线段会互相重合。为了更好地理解这一点，我们可以逐一分析这三条线段的性质及其重合的原因。

第一条线段是顶角的角平分线。角平分线的定义是将一个角分为两个相等的角，而等腰三角形的顶角平分线正是将顶角分为两个相等的底角。由于等腰三角形的两个底角已经相等，因此顶角的角平分线自然与底边平行，并且平分底边。

第二条线段是底边上的中线。中线是连接三角形任意两边中点的线段。在等腰三角形中，底边上的中线连接底边的两个中点，并且由于等腰三角形的对称性，这条中线会垂直于底边，将底边平分。

第三条线段是底边上的高线。高线是从三角形的一个顶点垂直于对边或对边的延长线所引的线段。在等腰三角形中，底边上的高线是从顶角垂直于底边所引的线段。由于等腰三角形的对称性，这条高线不仅垂直于底边，而且与底边上的中线重合。

现在，我们来探讨为什么这三条线段会重合。在等腰三角形中，由于两腰相等，顶角被平分，因此顶角的角平分线将底边平分。同时，由于等腰三角形的对称性，底边上的中线和高线都会垂直于底边，并且平分底边。因此，这三条线段在等腰三角形中实际上是同一条线段，即它们互相重合。

“三线合一”的性质在等腰三角形的证明和问题解决中具有广泛的应用。首先，它可以帮助我们添加辅助线，从而简化几何问题的求解过程。例如，在解决与等腰三角形相关的几何问题时，我们可以利用“三线合一”的性质来连接底边的中点与顶角，从而得到一条垂直于底边的线段，这对于证明三角形全等或求解线段长度等问题非常有帮助。

其次，“三线合一”的性质有助于证明三角形全等。在等腰三角形中，由于“三线合一”，我们可以很容易地证明两个三角形是全等的。例如，如果我们知道一个三角形是等腰三角形，并且知道其中一条线段是底边上的中线或高线，那么我们就可以利用“三线合一”的性质来证明这个三角形与另一个三角形是全等的。

此外，“三线合一”的性质还可以用于证明线段相等。在等腰三角形中，由于“三线合一”，我们可以很容易地证明两条线段是相等的。例如，如果我们知道一个三角形是等腰三角形，并且知道其中一条线段是底边上的中线或高线，那么我们就可以利用“三线合一”的性质来证明这条线段与另一条线段是相等的。

除了在数学中的应用外，“三线合一”的性质在物理学中也有重要的应用。特别是在光的反射与折射中，“三线合一”的概念得到了广泛的应用。在光的反射中，入射光线、法线和反射光线三线合一，这时入射角、反射角都是0度。这一性质在光学仪器的设计和制造中具有重要的指导意义。

综上所述，等腰三角形的“三线合一”是指顶角的角平分线、底边上的中线以及底边上的高线这三条线段互相重合。这一性质是等腰三角形独有的，对于非等腰三角形是不成立的。在等腰三角形的证明和问题解决中，“三线合一”的性质具有广泛的应用价值，它可以帮助我们添加辅助线、证明三角形全等以及证明线段相等。同时，“三线合一”的概念在物理学中也具有重要的应用意义。

因此，对于那些有兴趣了解等腰三角形“三线合一”是哪三线的用户来说，理解并掌握这一性质是非常重要的。通过深入学习和实践应用，“三线合一”将成为你解决几何问题和理解物理学原理的有力工具。希望本文能够帮助你更好地理解和掌握等腰三角形的“三线合一”性质。