揭秘：组合计算公式的详细解读

组合计算公式是数学中的一个基本概念，广泛应用于统计学、计算机科学、概率论等多个领域。它用于计算在给定数量的元素中，不考虑顺序地选取指定数量元素的组合方式的总数。为了更好地理解和应用这一概念，本文将详细介绍组合计算公式的原理、推导过程、具体计算方法以及其在现实生活中的应用。

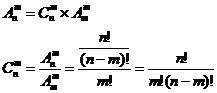
组合计算公式通常表示为C(n, k)或nCk，其中n表示总元素的数量，k表示要选取的元素数量。组合的本质是从n个不同元素中，不考虑元素的排列顺序，选出k个元素的所有可能方式。这与排列不同，排列需要考虑元素的顺序。因此，组合数通常小于或等于对应的排列数。

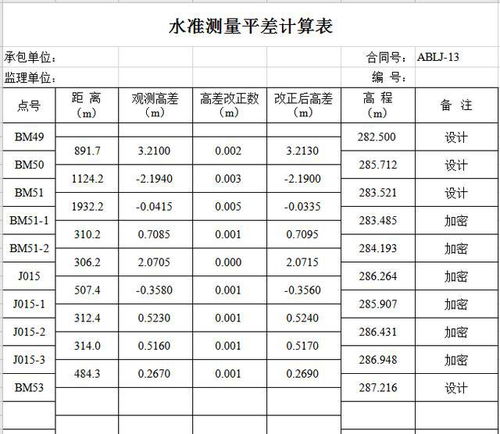
组合计算公式的具体形式是：

C(n, k) = n! / (k!(n-k)!)

其中，“!”表示阶乘，即一个数与它前面所有正整数的乘积。例如，5! = 5 × 4 × 3 × 2 × 1 = 120。

现在，我们来详细推导这个公式。假设有n个不同的元素，我们要从中选出k个元素形成一个组合。首先，我们可以从n个元素中任意选择一个作为组合的第一个元素，有n种选择。接着，从剩下的n-1个元素中选择第二个元素，有n-1种选择。依此类推，直到从剩下的n-k+1个元素中选择第k个元素，有n-k+1种选择。因此，如果考虑顺序，总的选择方式有n × (n-1) × ... × (n-k+1)种。

然而，组合是不考虑顺序的。例如，从{1, 2, 3}中选出两个元素的组合有{1, 2}和{2, 1}，但这两个组合在组合学中视为同一个组合。因此，我们需要去除所有可能的排列重复。对于k个元素，它们的排列方式有k!种。所以，最终的组合数应该是考虑顺序的选择方式除以k个元素的排列方式，即：

n × (n-1) × ... × (n-k+1) / k! = n! / (k!(n-k)!)

这就得到了我们熟悉的组合计算公式。

在实际应用中，组合计算公式可以用来解决许多实际问题。例如，在统计学中，我们经常需要从样本空间中随机抽取一定数量的样本进行研究。这时，组合公式可以帮助我们计算所有可能的抽样方式。在概率论中，组合公式用于计算基本事件的数量，从而确定事件的概率。在计算机科学中，组合公式在算法设计、数据结构选择等方面也有广泛应用。

此外，组合计算公式还可以与其他数学概念结合使用，形成更复杂的计算方法。例如，在组合数学中，我们经常需要计算多重组合（即允许重复选择元素）的数量。这时，组合公式需要稍作修改，以反映元素可以重复的事实。

除了基本的组合计算公式外，还有一些与之相关的组合恒等式和性质。这些恒等式和性质在组合数学中非常重要，它们可以简化计算过程，提高计算效率。例如，组合数的加法公式C(n, k) = C(n-1, k-1) + C(n-1, k)表明，从n个元素中选取k个元素的组合数等于从n-1个元素中选取k-1个元素的组合数与从n-1个元素中选取k个元素的组合数之和。这个恒等式在递归计算组合数时非常有用。

另一个重要的组合性质是帕斯卡恒等式C(n, k) = C(n-1, k-1) + C(n-k, k)，它表示从n个元素中选取k个元素的组合数等于从n-1个元素中不选取第n个元素而选取k-1个元素的组合数与从n-k个元素（包括第n个元素）中选取k个元素的组合数之和。这个恒等式在组合数的展开和证明中经常用到。

此外，组合计算公式还可以用于解决一些经典的数学问题。例如，在组合数学中，有一个著名的“鸽巢原理”问题：如果n个物体放入m个盒子中，且n > m，那么至少有一个盒子里包含两个或两个以上的物体。这个问题可以通过组合公式进行证明和求解。

总的来说，组合计算公式是数学中一个非常重要的概念，它为我们提供了一种计算从给定数量的元素中选取指定数量元素的所有可能方式的方法。通过理解和应用这个公式，我们可以更好地解决许多实际问题，并在数学、统计学、计算机科学等领域中取得更大的进展。

当然，组合计算公式并不是万能的。在实际应用中，我们还需要考虑问题的具体背景和要求，选择合适的数学模型和方法进行求解。同时，我们也需要不断学习新的数学知识和方法，以应对日益复杂的数学问题。通过不断学习和实践，我们可以更好地掌握组合计算公式的应用技巧和方法，提高自己的数学素养和解决问题的能力。