对角矩阵的秩：总是等于n的奥秘吗？

对角矩阵的秩是否为n的深入探讨

在数学领域，对角矩阵作为一种特殊的矩阵形式，具有许多独特的性质和广泛的应用。其中一个常见的问题是：对角矩阵的秩是否为n？为了回答这个问题，我们需要从多个维度进行深入探讨，包括对角矩阵的定义、性质、秩的概念，以及具体的例子和理论证明。

首先，我们来回顾一下对角矩阵的定义。对角矩阵（Diagonal Matrix）是一个主对角线之外的元素皆为0的矩阵。对角线上元素可以为0或其他值；对角线上元素相等的对角矩阵称为数量矩阵；对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵可以认为是矩阵中最简单的一种，值得一提的是：对角线上的元素可以为0或其他值；对角线上元素相等的对角矩阵称为数量矩阵；对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算，且结果仍为对角阵。

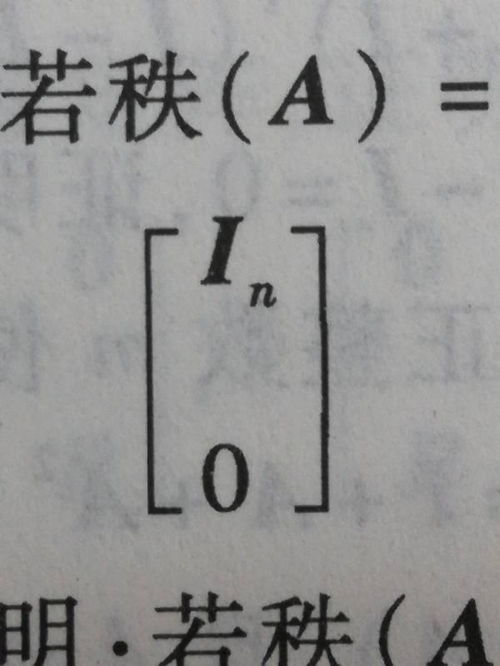
接下来，我们探讨一下对角矩阵的性质。对角矩阵的运算比一般的矩阵更为简单，值得注意的是：对角矩阵的幂运算等于主对角线上各个元素的相应次幂构成的对角矩阵；对角矩阵的逆运算只有当对角矩阵可逆时（即对角线上元素均不为0）才能进行，且其逆矩阵也是对角矩阵；两个同阶对角矩阵的乘积运算仍为对角矩阵，且其乘积主对角线上的各个元素等于原来两个对角矩阵主对角线上对应元素的乘积；对角矩阵的行列式等于主对角线上各个元素的乘积；对角矩阵是可逆的，当且仅当其对角线上的元素不等于0，其对角线上元素的乘积即为可逆矩阵的行列式值，且其逆矩阵仍为对角矩阵。这些性质使得对角矩阵在理论研究和实际应用中都显得尤为重要。

现在，我们来明确一下秩的概念。矩阵的秩是矩阵的一个重要属性，它反映了矩阵的某种本质特性。在数学上，矩阵的秩定义为矩阵中最大的非零子式的阶数。具体来说，如果矩阵A中存在一个r阶子式不为0，而所有r+1阶子式全为0，则称A的秩为r。矩阵的秩是矩阵的一个基本属性，它决定了矩阵的许多重要性质，如矩阵的线性相关性、可逆性、特征值等。同时，矩阵的秩也是矩阵分解、矩阵的秩分解、矩阵的满秩分解等理论的基础。

那么，对角矩阵的秩是多少呢？为了回答这个问题，我们需要从对角矩阵的性质出发进行分析。由于对角矩阵主对角线之外的元素皆为0，因此其非零子式只可能出现在主对角线上。换句话说，对角矩阵的秩等于其主对角线上非零元素的个数。当对角矩阵是n阶方阵时，如果其主对角线上的元素全部非零，那么该对角矩阵的秩就是n；如果主对角线上有k个非零元素（k

为了更具体地说明这个问题，我们可以举一个例子。假设有一个3阶对角矩阵A，其主对角线上的元素分别为a、b、c。如果a、b、c均不为0，那么矩阵A的秩为3；如果a=0，b≠0，c≠0，那么矩阵A的秩为2；如果a=b=0，c≠0，那么矩阵A的秩为1；如果a=b=c=0，那么矩阵A的秩为0。这个例子很好地说明了对角矩阵的秩与其主对角线上非零元素的个数之间的关系。

此外，我们还可以从线性代数的角度进一步理解这个问题。在线性代数中，矩阵的秩可以理解为矩阵所代表的线性变换的维度。对于对角矩阵来说，如果其主对角线上的元素全部非零，那么它代表的线性变换就是满秩的，即可以将n维空间中的任意向量映射到n维空间中的另一个向量；如果主对角线上有k个非零元素（k

综上所述，我们可以得出结论：对角矩阵的秩不一定为n，而是等于其主对角线上非零元素的个数。这个结论不仅适用于一般的对角矩阵，还适用于数量矩阵和单位矩阵等特殊类型的对角矩阵。在实际应用中，我们可以根据对角矩阵的秩来判断其代表的线性变换的维度和能力，从而进行相应的数学分析和计算。同时，这个结论也为矩阵的秩分解、矩阵的满秩分解等理论提供了重要的基础和依据。

最后，需要指出的是，虽然对角矩阵的秩不一定为n，但是对角矩阵在许多方面都具有独特的优势和广泛的应用。例如，在矩阵运算中，对角矩阵的乘法、幂运算等都比一般的矩阵更为简单和高效；在矩阵分解中，对角矩阵也是许多分解方法的重要组成部分